如何设计一个C++深度学习框架
本教程将指导你使用 C++ 和 Eigen 库,从零实现一个结构清晰、模块化的轻量级深度学习框架。该框架模仿 Keras 的 API 风格,适合学习深度学习底层原理与 C++ 工程实践。
前提要求:熟悉 C++ 基础语法,了解深度学习基本概念(如前向传播、反向传播、损失函数、优化器等)。
框架概览
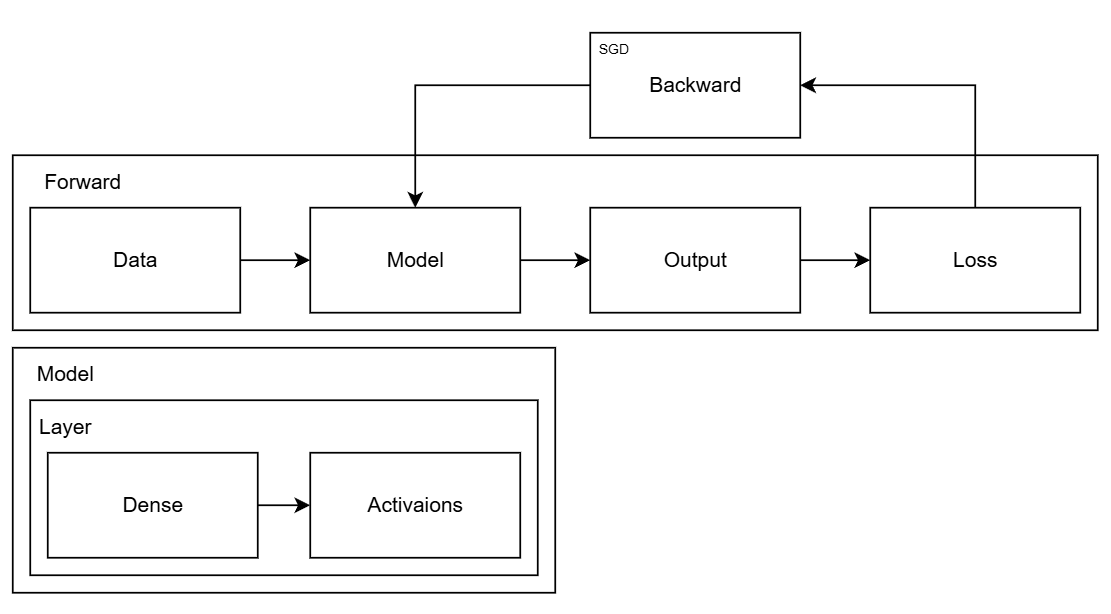
我们要实现的深度学习框架大致包括以下模块:
- Layer(神经网络层):神经网络层的抽象基类,定义前向传播、反向传播和参数更新接口。
- Activation(激活函数):激活函数层(如 ReLU、Sigmoid),作为无参
Layer的特例 - Loss(损失函数):损失函数(如 MSE、交叉熵),用于计算预测误差及其梯度。
- Optimizer(优化器):优化器(如 SGD),负责根据梯度更新模型参数。
- Sequential(顺序模型):顺序模型容器,用于堆叠多层网络并统一管理训练流程。
设计原则
- 模块解耦:每一层(包括激活函数)都继承自
Layer,独立实现forward()和backward()。 - 无状态训练:训练过程由
Sequential::train_step()驱动,依次调用各层的前向/反向传播。 - 参数管理:只有含可训练参数的层(如全连接层)实现
apply_optimizer();激活函数等无参层无需此方法。 - 梯度流清晰:损失函数不仅返回标量损失值,还提供对预测输出的梯度,作为反向传播起点
工作流程
- 用户通过
Sequential按顺序添加Dense构建模型。 调用
model.train_step(X, y)开始一次训练迭代:- 前向传播:逐层计算输出,最终得到预测值
y_pred。 - 损失计算:调用
Loss::compute(y_pred, y)得到损失值和 梯度dL/dy_pred。 - 反向传播:从最后一层开始,将梯度逐层反传,每层计算自身参数梯度。
- 参数更新:对含参层调用
apply_optimizer(),使用Optimizer更新权重与偏置。
- 前向传播:逐层计算输出,最终得到预测值
1. Layer:神经网络层基类
Layer 是所有神经网络层的基类,它定义了每一层必须实现的接口:
#pragma once
#include <Eigen/Dense>
struct Layer {
virtual Eigen::MatrixXf forward(const Eigen::MatrixXf& input) = 0;
virtual Eigen::MatrixXf backward(const Eigen::MatrixXf& grad_output) = 0;
virtual void apply_optimizer(class Optimizer& opt) = 0;
virtual ~Layer() = default;
};- forward:计算该层的输出。输入维度为
[输入特征数, 样本数],输出维度为[输出特征数, 样本数]。 - backward:根据上一层的梯度计算该层的梯度,并传递给前一层。
- apply_optimizer:使用优化器更新可训练参数。
2. Dense:全连接层
Dense 层实现了全连接层(Fully Connected Layer),公式为:
$$ \text{output} = W \cdot \text{input} + b $$
#pragma once
#include "Layer.h"
#include "Optimizer.h"
/**
* Dense类:全连接层
*
* 该类实现了神经网络中的全连接层
*/
struct Dense : Layer {
// 输入特征维度和输出特征维度
int in_dim, out_dim;
// 权重矩阵及其梯度和动量
Eigen::MatrixXf W, gradW, velocityW;
// 偏置向量及其梯度和动量
Eigen::VectorXf b, gradb, velocityb;
// 缓存前向传播的输入数据,用于反向传播计算
Eigen::MatrixXf input_cache;
/**
* Dense层构造函数
*
* @param in_dim_ 输入特征维度
* @param out_dim_ 输出特征维度
*/
Dense(int in_dim_, int out_dim_);
/**
* 前向传播计算
*
* 计算公式:output = W * input + b
*
* @param input 输入数据,维度为[in_dim, 样本数]
* @return 层的输出,维度为[out_dim, 样本数]
*/
Eigen::MatrixXf forward(const Eigen::MatrixXf& input) override;
/**
* 反向传播计算
*
* 计算权重和偏置的梯度,并返回传递给下一层的梯度
*
* @param grad_output 来自上一层的梯度,维度为[out_dim, 样本数]
* @return 传递给下一层的梯度,维度为[in_dim, 样本数]
*/
Eigen::MatrixXf backward(const Eigen::MatrixXf& grad_output) override;
/**
* 应用优化器更新层的参数
*
* @param opt 优化器对象,用于更新权重和偏置
*/
void apply_optimizer(Optimizer& opt) override;
};
#include "Dense.h"
#include "Utils.h"
#include <cassert>
/**
* Dense层构造函数
*
* 初始化层的参数,包括权重矩阵和偏置向量
* 权重矩阵使用Xavier初始化方法,偏置向量初始化为0
*
* @param in_dim_ 输入特征维度
* @param out_dim_ 输出特征维度
*/
Dense::Dense(int in_dim_, int out_dim_)
: in_dim(in_dim_), out_dim(out_dim_),
W(out_dim_, in_dim_), gradW(out_dim_, in_dim_), velocityW(Eigen::MatrixXf::Zero(out_dim_, in_dim_)),
b(out_dim_), gradb(out_dim_), velocityb(Eigen::VectorXf::Zero(out_dim_))
{
// 使用Xavier初始化方法初始化权重矩阵
xavier_init(W);
// 偏置向量初始化为0
b.setZero();
}
/**
* 前向传播计算
*
* 实现全连接层的前向传播,计算公式为:output = W * input + b
*
* @param input 输入数据,维度为[in_dim, 样本数]
* @return 层的输出,维度为[out_dim, 样本数]
*/
Eigen::MatrixXf Dense::forward(const Eigen::MatrixXf& input) {
// 缓存输入数据,用于反向传播计算
input_cache = input;
// 计算线性变换:W * input
Eigen::MatrixXf out = W * input;
// 对每一列(每个样本)加上偏置向量
out.colwise() += b;
return out;
}
/**
* 反向传播计算
*
* 计算权重和偏置的梯度,并返回传递给前一层的梯度
*
* @param grad_output 来自上一层的梯度,维度为[out_dim, 样本数]
* @return 传递给下一层的梯度,维度为[in_dim, 样本数]
*/
Eigen::MatrixXf Dense::backward(const Eigen::MatrixXf& grad_output) {
// 获取批次大小
int batch = grad_output.cols();
// 计算权重梯度:gradW = (grad_output * input_cache^T) / batch
// 除以批次大小是为了平均梯度
gradW = (grad_output * input_cache.transpose()) / float(batch);
// 计算偏置梯度:对每个输出神经元,计算所有样本的平均梯度
gradb = grad_output.rowwise().mean();
// 计算传递给前一层的梯度:W^T * grad_output
return W.transpose() * grad_output;
}
/**
* 应用优化器更新层的参数
*
* 分别对权重矩阵和偏置向量应用优化器进行更新
*
* @param opt 优化器对象,用于更新权重和偏置
*/
void Dense::apply_optimizer(Optimizer& opt) {
// 更新权重矩阵
opt.step(W, gradW, velocityW);
// 更新偏置向量
opt.step(b, gradb, velocityb);
}
- 权重初始化:使用 Xavier 初始化以缓解梯度消失/爆炸问题。
- 前向传播:
output = W * input + b,同时缓存输入用于反向传播。 - 反向传播:计算梯度
gradW和gradb,并传递梯度给前一层。 - 参数更新:通过优化器更新权重和偏置。
3. Activation:激活函数层
ReLU
ReLU 层的前向传播为 f(x) = max(0, x),反向传播只传递激活的神经元梯度。
/**
* ReLU类:修正线性单元激活函数层的实现
*
* ReLU激活函数定义为:f(x) = max(0, x)
* 它是一种常用的非线性激活函数,有助于缓解梯度消失问题
*/
struct ReLU : Layer {
// 用于存储前向传播中哪些神经元被激活的掩码
Eigen::MatrixXf mask;
/**
* 前向传播计算
*
* 实现ReLU激活函数:output = max(0, input)
*
* @param input 输入数据,维度为[特征数, 样本数]
* @return 激活后的输出,维度与输入相同
*/
Eigen::MatrixXf forward(const Eigen::MatrixXf& input) override;
/**
* 反向传播计算
*
* ReLU的导数:如果输入大于0则导数为1,否则为0
*
* @param grad_output 来自上一层的梯度,维度与输入相同
* @return 传递给下一层的梯度,维度与输入相同
*/
Eigen::MatrixXf backward(const Eigen::MatrixXf& grad_output) override;
/**
* 应用优化器更新参数
*
* ReLU层没有可训练参数,所以这个方法为空
*/
void apply_optimizer(class Optimizer& opt) override {}
};
/**
* ReLU前向传播计算
*
* 实现ReLU激活函数:output = max(0, input)
* 同时创建一个掩码,记录哪些神经元被激活(输入大于0)
*
* @param input 输入数据,维度为[特征数, 样本数]
* @return 激活后的输出,维度与输入相同
*/
Eigen::MatrixXf ReLU::forward(const Eigen::MatrixXf& input) {
// 创建掩码:输入大于0的位置为1,否则为0
mask = (input.array() > 0).cast<float>();
// 应用ReLU:只保留输入中大于0的部分
return input.array() * mask.array();
}
/**
* ReLU反向传播计算
*
* ReLU的导数:如果输入大于0则导数为1,否则为0
* 使用前向传播时保存的掩码来计算梯度
*
* @param grad_output 来自上一层的梯度,维度与输入相同
* @return 传递给下一层的梯度,维度与输入相同
*/
Eigen::MatrixXf ReLU::backward(const Eigen::MatrixXf& grad_output) {
// 梯度乘以掩码:只传递激活神经元的梯度
return grad_output.array() * mask.array();
}Sigmoid
Sigmoid 层前向传播为 f(x) = 1 / (1 + exp(-x)),反向传播为 f'(x) = f(x) * (1 - f(x))。
/**
* Sigmoid类:Sigmoid激活函数层的实现
*
* Sigmoid激活函数定义为:f(x) = 1 / (1 + exp(-x))
* 它将输入映射到(0, 1)区间,常用于二分类问题的输出层
*/
struct Sigmoid : Layer {
// 缓存前向传播的输出,用于反向传播计算
Eigen::MatrixXf output_cache;
/**
* 前向传播计算
*
* 实现Sigmoid激活函数:output = 1 / (1 + exp(-input))
*
* @param input 输入数据,维度为[特征数, 样本数]
* @return 激活后的输出,维度与输入相同
*/
Eigen::MatrixXf forward(const Eigen::MatrixXf& input) override;
/**
* 反向传播计算
*
* Sigmoid的导数:f'(x) = f(x) * (1 - f(x))
*
* @param grad_output 来自上一层的梯度,维度与输入相同
* @return 传递给下一层的梯度,维度与输入相同
*/
Eigen::MatrixXf backward(const Eigen::MatrixXf& grad_output) override;
/**
* 应用优化器更新参数
*
* Sigmoid层没有可训练参数,所以这个方法为空
*/
void apply_optimizer(class Optimizer& opt) override {}
};
/**
* Sigmoid前向传播计算
*
* 实现Sigmoid激活函数:output = 1 / (1 + exp(-input))
* 缓存输出结果,用于反向传播计算
*
* @param input 输入数据,维度为[特征数, 样本数]
* @return 激活后的输出,维度与输入相同
*/
Eigen::MatrixXf Sigmoid::forward(const Eigen::MatrixXf& input) {
// 计算Sigmoid输出:1/(1+exp(-input))
output_cache = (1.0f + (-input.array()).exp()).inverse();
return output_cache;
}
/**
* Sigmoid反向传播计算
*
* Sigmoid的导数:f'(x) = f(x) * (1 - f(x))
* 使用前向传播时保存的输出缓存来计算梯度
*
* @param grad_output 来自上一层的梯度,维度与输入相同
* @return 传递给下一层的梯度,维度与输入相同
*/
Eigen::MatrixXf Sigmoid::backward(const Eigen::MatrixXf& grad_output) {
// 梯度乘以Sigmoid的导数:f'(x) = f(x) * (1 - f(x))
return grad_output.array() * (output_cache.array() * (1 - output_cache.array()));
}Softmax
Softmax 层用于多分类输出,将 logits 转换为概率分布:
$$ \text{softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}} $$
/**
* softmax函数的实现
*
* 将原始得分(logits)转换为概率分布
* 为了数值稳定性,使用了最大值归一化技巧
*
* @param logits 原始得分(未归一化的对数概率)
* @return 归一化后的概率分布,维度与输入相同
*/
Eigen::MatrixXf Softmax::softmax(const Eigen::MatrixXf& logits) {
// 创建输出矩阵
Eigen::MatrixXf out = logits;
// 对每个样本(每一列)单独应用softmax
for (int c = 0; c < logits.cols(); ++c) {
// 获取当前样本的最大值,用于数值稳定性
float m = logits.col(c).maxCoeff();
// 计算指数,减去最大值以避免数值溢出
Eigen::VectorXf exps = (logits.col(c).array() - m).exp();
// 归一化,使所有概率之和为1
out.col(c) = exps / exps.sum();
}
return out;
}4. Loss:损失函数
均方误差(MSE)
用于回归任务:
公式如下
$$ \text{MSE} = \frac{1}{2N} \sum (y_{\text{pred}} - y_{\text{true}})^2 $$
/**
* LossResult结构体:损失函数计算结果的容器
*
* 包含损失值和梯度信息,用于训练神经网络
*/
struct LossResult {
// 损失值,表示预测值与目标值之间的差距
float loss;
// 损失函数对模型输出的梯度,用于反向传播
Eigen::MatrixXf grad;
};
/**
* 均方误差(MSE)损失函数
*
* 计算公式:MSE = (1/(2*N)) * sum((preds - targets)^2)
* 常用于回归问题
*
* @param preds 模型的预测值,维度为[输出特征数, 样本数]
* @param targets 目标值,维度与预测值相同
* @return LossResult结构体,包含损失值和梯度
*/
LossResult mse_loss(const Eigen::MatrixXf& preds, const Eigen::MatrixXf& targets);
/**
* 均方误差(MSE)损失函数实现
*
* 计算公式:MSE = (1/(2*N)) * sum((preds - targets)^2)
* 常用于回归问题
*
* @param preds 模型的预测值,维度为[输出特征数, 样本数]
* @param targets 目标值,维度与预测值相同
* @return LossResult结构体,包含损失值和梯度
*/
LossResult mse_loss(const Eigen::MatrixXf& preds, const Eigen::MatrixXf& targets) {
// 检查预测值和目标值的维度是否匹配
assert(preds.rows() == targets.rows() && preds.cols() == targets.cols() && "Dimensions of predictions and targets must match");
// 计算预测值和目标值之间的差异
Eigen::MatrixXf diff = preds - targets;
// 计算样本数
float num_samples = preds.cols();
// 计算损失值:(1/(2*N)) * sum((preds - targets)^2)
float loss = diff.array().square().sum() / (2.0f * num_samples);
// 计算梯度:(preds - targets) / N
Eigen::MatrixXf grad = diff / num_samples;
// 返回损失结果
return {loss, grad};
}Softmax 交叉熵
用于多分类任务,结合 Softmax 输出和交叉熵损失:
$$ \text{CE} = - \sum y_{\text{true}} \cdot \log(\text{softmax}(y_{\text{pred}})) $$
/**
* Softmax交叉熵损失函数
*
* 结合了softmax函数和交叉熵损失,常用于多分类问题
* 计算公式:CE = -sum(targets * log(softmax(logits)))
*
* @param logits 模型的原始输出(未经过softmax)
* @param onehot_targets 独热编码的目标标签
* @return LossResult结构体,包含损失值和梯度
*/
LossResult softmax_cross_entropy(const Eigen::MatrixXf& logits, const Eigen::MatrixXf& onehot_targets);
/**
* Softmax交叉熵损失函数实现
*
* 结合了softmax函数和交叉熵损失,常用于多分类问题
* 计算公式:CE = -sum(targets * log(softmax(logits)))
*
* @param logits 模型的原始输出(未经过softmax)
* @param onehot_targets 独热编码的目标标签
* @return LossResult结构体,包含损失值和梯度
*/
LossResult softmax_cross_entropy(const Eigen::MatrixXf& logits, const Eigen::MatrixXf& onehot_targets) {
// 检查logits和目标标签的维度是否匹配
assert(logits.rows() == onehot_targets.rows() && logits.cols() == onehot_targets.cols() && "Dimensions of logits and targets must match");
// 应用softmax函数将logits转换为概率分布
Eigen::MatrixXf probs = Softmax::softmax(logits);
// 添加一个小的epsilon值以避免log(0)的情况
const float epsilon = 1e-8f;
Eigen::MatrixXf log_probs = (probs.array() + epsilon).log();
// 计算样本数
float num_samples = logits.cols();
// 计算交叉熵损失:-sum(targets * log(probs)) / N
float loss = - (onehot_targets.array() * log_probs.array()).sum() / num_samples;
// softmax交叉熵的梯度简化计算:probs - targets
Eigen::MatrixXf grad = (probs - onehot_targets) / num_samples;
// 返回损失结果
return {loss, grad};
}5. Optimizer:优化器
SGD(随机梯度下降)支持动量:
#pragma once
#include <Eigen/Dense>
/**
* Optimizer类:优化器的抽象基类
*
* 所有具体的优化器都必须继承自这个基类,
* 并实现更新矩阵参数和向量参数的方法。
*/
struct Optimizer {
/**
* 更新矩阵参数的方法
*
* @param W 要更新的矩阵参数(如权重矩阵)
* @param gradW 参数的梯度
* @param velocityW 用于动量优化的速度项
*/
virtual void step(Eigen::MatrixXf& W, const Eigen::MatrixXf& gradW, Eigen::MatrixXf& velocityW) = 0;
/**
* 更新向量参数的方法
*
* @param b 要更新的向量参数(如偏置向量)
* @param gradb 参数的梯度
* @param velocityb 用于动量优化的速度项
*/
virtual void step(Eigen::VectorXf& b, const Eigen::VectorXf& gradb, Eigen::VectorXf& velocityb) = 0;
// 虚析构函数,确保派生类对象被正确销毁
virtual ~Optimizer() = default;
};
/**
* SGD类:随机梯度下降优化器的实现
*
* 支持基本的随机梯度下降和带动量的随机梯度下降
* 动量可以加速训练并减少震荡
*/
struct SGD : Optimizer {
// 学习率:控制参数更新的步长
float lr;
// 动量因子:控制历史梯度的影响程度
float momentum;
/**
* SGD优化器构造函数
*
* @param lr_ 学习率,默认为0.01
* @param momentum_ 动量因子,默认为0.0(无动量)
*/
SGD(float lr_=0.01f, float momentum_=0.0f): lr(lr_), momentum(momentum_) {}
/**
* 更新矩阵参数
*
* @param W 要更新的矩阵参数(如权重矩阵)
* @param gradW 参数的梯度
* @param velocityW 用于动量优化的速度项
*/
void step(Eigen::MatrixXf& W, const Eigen::MatrixXf& gradW, Eigen::MatrixXf& velocityW) override;
/**
* 更新向量参数
*
* @param b 要更新的向量参数(如偏置向量)
* @param gradb 参数的梯度
* @param velocityb 用于动量优化的速度项
*/
void step(Eigen::VectorXf& b, const Eigen::VectorXf& gradb, Eigen::VectorXf& velocityb) override;
};
#include "Optimizer.h"
/**
* 更新矩阵参数(如权重矩阵)
*
* 根据是否使用动量,实现两种不同的更新策略:
* 1. 带动量:velocity = momentum * velocity - lr * grad
* W = W + velocity
* 2. 无动量:W = W - lr * grad
*
* @param W 要更新的矩阵参数(如权重矩阵)
* @param gradW 参数的梯度
* @param velocityW 用于动量优化的速度项
*/
void SGD::step(Eigen::MatrixXf &W, const Eigen::MatrixXf &gradW, Eigen::MatrixXf &velocityW)
{
// 更新动量项: velocity = momentum * velocity - lr * grad
if (momentum > 0.0f)
{
velocityW = momentum * velocityW - lr * gradW;
// 更新参数: W = W + velocity
W += velocityW;
}
else
{
// 无动量情况: W = W - lr * gradW
W -= lr * gradW;
}
}
/**
* 更新向量参数(如偏置向量)
*
* 根据是否使用动量,实现两种不同的更新策略:
* 1. 带动量:velocity = momentum * velocity - lr * grad
* b = b + velocity
* 2. 无动量:b = b - lr * grad
*
* @param b 要更新的向量参数(如偏置向量)
* @param gradb 参数的梯度
* @param velocityb 用于动量优化的速度项
*/
void SGD::step(Eigen::VectorXf &b, const Eigen::VectorXf &gradb, Eigen::VectorXf &velocityb)
{
// 更新动量项: velocity = momentum * velocity - lr * grad
if (momentum > 0.0f)
{
velocityb = momentum * velocityb - lr * gradb;
// 更新参数: b = b + velocity
b += velocityb;
}
else
{
// 无动量情况: b = b - lr * gradb
b -= lr * gradb;
}
}- 带动量:
velocity = momentum * velocity - lr * grad,param += velocity - 不带动量:
param -= lr * grad
6. Sequential:模型类
Sequential 类用于按顺序堆叠各层:
#pragma once
#include <vector>
#include <memory>
#include "Layer.h"
#include "Loss.h"
#include "Optimizer.h"
/**
* Sequential类:线性堆叠的神经网络模型
*
* 这个类实现了一个简单的前馈神经网络,支持按顺序添加各种层,
* 并提供前向传播预测和单步训练功能。
*/
struct Sequential {
// 存储神经网络的所有层
std::vector<std::shared_ptr<Layer>> layers;
/**
* 向模型添加一个新的神经网络层
*
* @param layer 要添加的层的智能指针
*/
void add(std::shared_ptr<Layer> layer);
/**
* 使用模型进行前向传播预测
*
* @param X 输入数据,维度为[特征数, 样本数]
* @return 输出预测结果,维度取决于最后一层的输出
*/
Eigen::MatrixXf predict(const Eigen::MatrixXf& X);
/**
* 执行单步训练,包括前向传播、损失计算、反向传播和参数更新
*
* @param X 输入数据,维度为[特征数, 样本数]
* @param Y 目标标签,如果是分类问题应为one-hot编码
* @param opt 优化器,用于更新模型参数
* @param is_classification 是否为分类问题,默认为true
* @return 当前训练步的损失值
*/
float train_step(const Eigen::MatrixXf& X, const Eigen::MatrixXf& Y, Optimizer& opt, bool is_classification=true);
};
#include "Sequential.h"
#include "Activations.h"
/**
* 向模型添加一个新的神经网络层
*
* @param layer 要添加的层的智能指针
*/
void Sequential::add(std::shared_ptr<Layer> layer)
{
// 将层添加到层列表的末尾
layers.push_back(layer);
}
/**
* 使用模型进行前向传播预测
*
* 该方法按顺序通过所有层执行前向传播计算,
* 从输入数据开始,到最后一层输出结束。
*
* @param X 输入数据,维度为[特征数, 样本数]
* @return 输出预测结果,维度取决于最后一层的输出
*/
Eigen::MatrixXf Sequential::predict(const Eigen::MatrixXf &X)
{
// 初始化输出为输入数据
Eigen::MatrixXf out = X;
// 按顺序通过每一层执行前向传播
for (auto &l : layers)
{
out = l->forward(out);
}
return out;
}
/**
* 执行单步训练,包括前向传播、损失计算、反向传播和参数更新
*
* 这个方法实现了完整的训练步骤:
* 1. 前向传播:通过所有层计算预测值
* 2. 损失计算:根据预测值和目标值计算损失及梯度
* 3. 反向传播:从最后一层开始,反向计算每一层的梯度
* 4. 参数更新:使用优化器更新所有可训练层的参数
*
* @param X 输入数据,维度为[特征数, 样本数]
* @param Y 目标标签,如果是分类问题应为one-hot编码
* @param opt 优化器,用于更新模型参数
* @param is_classification 是否为分类问题,默认为true
* @return 当前训练步的损失值
*/
float Sequential::train_step(const Eigen::MatrixXf &X, const Eigen::MatrixXf &Y, Optimizer &opt, bool is_classification)
{
// 1. 前向传播
Eigen::MatrixXf out = predict(X);
// 2. 计算损失和梯度
// 根据是否为分类问题选择不同的损失函数
LossResult lossres = is_classification ? softmax_cross_entropy(out, Y) : mse_loss(out, Y);
// 3. 反向传播
// 从损失函数的梯度开始,反向传播更新每一层的梯度
Eigen::MatrixXf grad = lossres.grad;
for (int i = (int)layers.size() - 1; i >= 0; --i)
{
grad = layers[i]->backward(grad);
}
// 4. 参数更新
// 对每一层应用优化器,更新可训练参数
for (auto &l : layers)
{
l->apply_optimizer(opt);
}
// 返回当前训练步的损失值
return lossres.loss;
}
- predict:按顺序执行每一层的前向传播。
train_step:
- 前向传播得到预测值。
- 根据任务类型计算损失和梯度。
- 反向传播梯度。
- 使用优化器更新参数。
7. 工具函数
- Xavier 初始化:用于初始化权重。
- onehot将标签向量转换为独热编码矩阵
#pragma once
#include <Eigen/Dense>
#include <random>
/**
* Xavier权重初始化方法
*
* 根据Glorot等人提出的初始化方法,用于缓解梯度消失/爆炸问题
* 权重值从均匀分布U[-√(6/(fan_in+fan_out)), √(6/(fan_in+fan_out))]中采样
*
* @param W 要初始化的权重矩阵
*/
inline void xavier_init(Eigen::MatrixXf& W) {
// 使用固定种子的随机数生成器,确保结果可重现
static std::mt19937 rng(1234);
// 获取输入特征数(fan_in)和输出特征数(fan_out)
float fan_in = W.cols(), fan_out = W.rows();
// 计算均匀分布的边界值
float limit = std::sqrt(6.0f / (fan_in + fan_out));
// 创建均匀分布
std::uniform_real_distribution<float> dist(-limit, limit);
// 为权重矩阵的每个元素分配随机值
for (int i = 0; i < W.size(); ++i) {
W.data()[i] = dist(rng);
}
}
/**
* 将标签向量转换为独热编码矩阵
*
* 独热编码是一种将分类标签转换为二进制向量的方法,
* 对于第i个样本,如果其标签为c,则输出矩阵的(c,i)位置为1,其余为0
*
* @param labels 标签向量,每个元素表示一个样本的类别索引
* @param num_classes 类别总数
* @return 独热编码矩阵,维度为[num_classes, 样本数]
*/
inline Eigen::MatrixXf to_one_hot(const Eigen::VectorXf& labels, int num_classes) {
// 获取样本数量
int batch = labels.size();
// 创建全零矩阵,用于存储独热编码结果
Eigen::MatrixXf onehot = Eigen::MatrixXf::Zero(num_classes, batch);
// 为每个样本设置对应的独热编码
for (int i = 0; i < batch; ++i) {
// 将标签转换为整数类别索引
int class_idx = static_cast<int>(labels(i));
// 设置对应位置为1
onehot(class_idx, i) = 1.0f;
}
return onehot;
}

1 条评论
膜拜大佬orz