Rosenblatt感知器，感知器也叫预测机

那么感知器有什么用呢？感知器可以拟合任何的线性函数，任何线性分类或线性回归问题都可以用感知器来解决。

使用python实现Rosenblatt感知器

pass：此次python实验的预测函数不含偏置项系数，所以函数图像过原点，只能拟合因果是成正比的数据或只能完成可被过原点的直线分类的数据

算法图

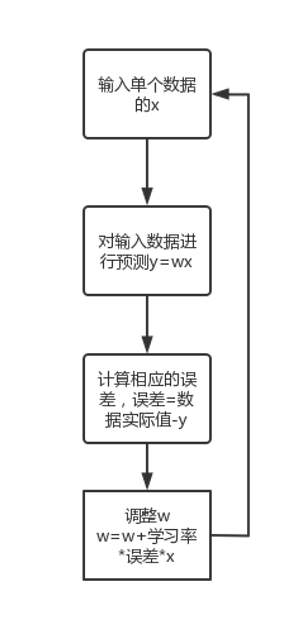
线性回归问题

1. 首先先引入需要用到的库

   import numpy
   from matplotlib import pypolt 

   引入numpy数学库以方便我们的数学计算

   引入matplotlib中的pyplot模块进行画图操作

   numpy使用手册：https://www.numpy.org.cn/

   matplotlib使用手册：https://www.matplotlib.org.cn/

2. 获取数据以便进行训练

   def getdata(count):
       """获取指定数量的数据"""
       x = np.random.rand(count)#生成区间[0,1)的随机数
       x = np.sort(x)#进行从小到大排序
       y = [1.5*xx+np.random.rand()/3 for xx in x]#使用列表推导式生成对应的值
       return x,y

   创建一个名为getdata的函数随机生成有共同特征的数据，有一个参数count来接收获取数据的数量

3. 获取100个数据

   xs,ys = getdata(100)#获取100个数据

4. 编写预测函数

   w = float("%.2f"%np.random.uniform(0,1))#随机生成权重参数
   alpha = 0.05#设置学习率
   y_predict =  w*xs#简单的预测函数

5. 绘制图像以便我们观察

   plt.scatter(xs,ys)#绘制散点图
   plt.plot(xs,y_predict)#绘制预测函数的图像
   plt.show()#显示图像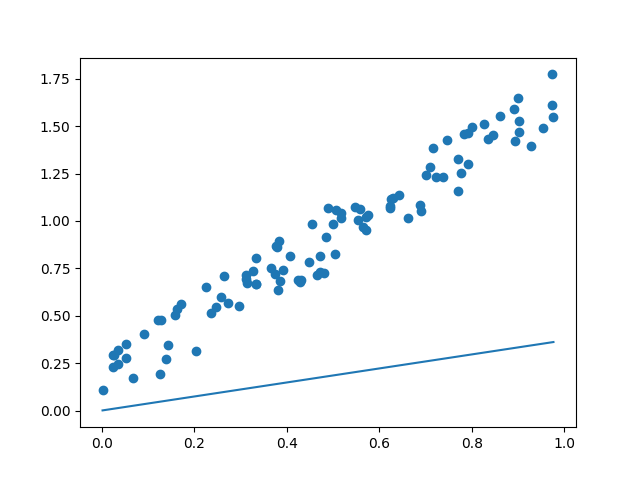

   

6. 算法的实现

   for i in range(100):#对每个数据进行一次权重调整
           x = xs[i]
           y = ys[i]
           #取出一个数据
           y_predict =  w*x#计算相应数据的预测值
           e = y - y_predict#计算相应数据的预测值与实际值的误差（使用差值评估误差）
           w = w + alpha*e*xs#根据误差调整权重参数
           y_predict = w * xs#重新配置预测函数

7. 多次训练

   why：因为学习率的存在，我们的预测函数只进行了一次在总体上的调整，无法完美的拟合。但是如果学习率设置太大会造成预测曲线不能收敛

   for _ in range(100):#进行100次训练
       for i in range(100):#对每个数据进行一次权重调整
           x = xs[i]
           y = ys[i]
           #取出一个数据
           y_predict =  w*x#计算相应数据的预测值
           e = y - y_predict#计算相应数据的预测值与实际值的误差（使用差值评估误差）
           w = w + alpha*e*xs#根据误差调整权重参数
           y_predict = w * xs#重新配置预测函数

8. 再次画出预测曲线

   plt.plot(xs,y_predict)#绘制预测函数的图像
   plt.show()#显示图像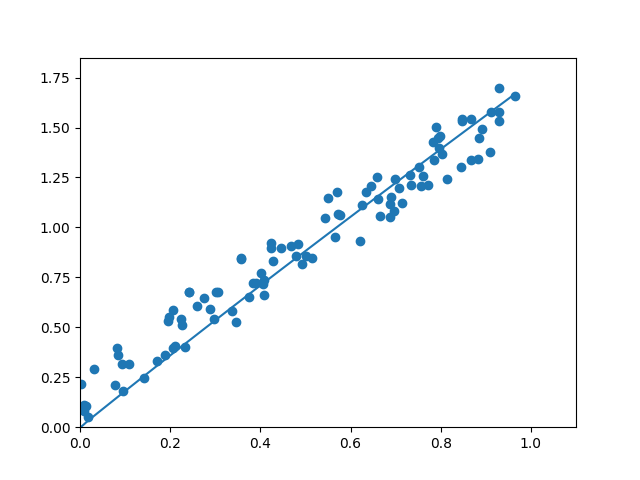

   

   可以看到完美的拟合了数据

线性回归问题代码

import numpy as np#引入numpy数学计算库
from matplotlib import pyplot as plt#引入matplotlib画图库

def getdata(count):
    """获取指定数量的数据"""
    x = np.random.rand(count)
    x = np.sort(x)
    y = [1.5*xx+np.random.rand()/3 for xx in x]
    return x,y

xs,ys = getdata(100)#获取100个数据

w = float("%.2f"%np.random.uniform(0,1))#随机生成权重参数
alpha = 0.05#设置学习率
y_predict =  w*xs#简单的预测函数

plt.scatter(xs,ys)#绘制散点图
plt.plot(xs,y_predict)#绘制预测函数的图像
plt.show()

for _ in range(100):#进行100次训练
    for i in range(100):#对每个数据进行一次权重调整
        x = xs[i]
        y = ys[i]
        #取出一个数据
        y_predict =  w*x#计算相应数据的预测值
        e = y - y_predict#计算相应数据的预测值与实际值的误差（使用差值评估误差）
        w = w + alpha*e*xs#根据误差调整权重参数
        y_predict = w * xs#重新配置预测函数
    #画图
    plt.clf()
    plt.xlim(0,1.1)
    plt.ylim(0,1.85)
    plt.scatter(xs,ys)
    plt.plot(xs,y_predict)
    plt.pause(0.01)
   
plt.show()