碰撞约束

在碰撞分离阶段除了使用碰撞法线直接分离物体之外，还有一种广泛用于各大刚体模拟引擎中的方法——碰撞约束。使用碰撞约束可以更加优雅的分离物体。

通过之前《物理引擎中的约束》这篇文章我们了解到我们只需要写出我们需要的约束方程，然后找出Jacobian矩阵就可以通过之前那篇文章最后导出的公式求解冲量了。接下来我们将介绍解释碰撞约束的约束方程和推导Jacobian矩阵。

碰撞约束的约束方程

假设物体A与物体B发生碰撞

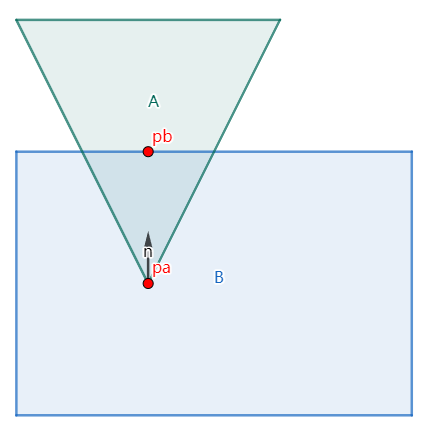
想一想我们需要什么效果，我们希望物体A与物体B满足分离状态，我们需要使用符号表示出这个状态。这里再次给出约束方程的含义：约束方程是用于描述一个系统中各部件之间相对运动限制的数学表达式。通过这些方程，我们可以定义哪些运动是允许的，哪些是被禁止的。即当方程中的参数满足约束方程我们就不必调整物体状态，否则我们需要调整物体状态。

所以我们可以这么定义碰撞约束的位置约束方程

$$ C = (\mathbf{P}_a-\mathbf{P}_b)\cdot\mathbf{n}\ge0 $$

这个方程表示两点在法向方向上不能穿透（距离 ≥ 0），但可以分离（距离 > 0）或者接触（距离=0）。还可以这么理解当两个物体穿透的时候$$\mathbf{P}_a-\mathbf{P}_b$$与法线的点积小于0（不满足约束方程）剩下的情况（ ≥ 0）就是满足约束的情况了。

找到约束方程后我们还需要找到Jacobian矩阵

Jacobian矩阵

还记得我们《物理引擎中的约束》中提到的我们找到位置约束方程后，我们还需要对时间求导，得到速度约束方程。

对上面得到的碰撞约束方程对时间求一阶导数得到速度约束方程

$$ \dot{C} = \mathbf{n}\cdot\frac{d}{dt}\mathbf{P}_a- \mathbf{n}\cdot\frac{d}{dt}\mathbf{P}_b $$

• $ \frac{d}{dt}\mathbf{P}_a$就是碰撞点a的速度
• $ \frac{d}{dt}\mathbf{P}_b$就是碰撞点b的速度

容易得到点a的速度为

$$ \frac{d}{dt}\mathbf{P}_a=\mathbf{v}_a+(\omega_a\times\mathbf{r}_a) $$

容易得到点b的速度为

$$ \frac{d}{dt}\mathbf{P}_b=\mathbf{v}_b+(\omega_b\times\mathbf{r}_b) $$

带入速度约束方程化简有

$$ \dot{C} = \mathbf{n}\cdot\mathbf{v}_a+\omega_a\cdot(\mathbf{r}_a\times\mathbf{n})-\mathbf{n}\cdot\mathbf{v}_b-\omega_b\cdot(\mathbf{r}_b\times\mathbf{n}) $$

我们将其写成矩阵的形式

$$ \dot{C} = \begin{bmatrix} \mathbf{n} & \mathbf{r}_a\times\mathbf{n} & -n &-\mathbf{r}_b\times\mathbf{n} \end{bmatrix}\begin{bmatrix} \mathbf{v}_a \\ \omega_a\\ \mathbf{v}_b \\ \omega_b \end{bmatrix} $$

其中Jacobian就是

$$ J=\begin{bmatrix} \mathbf{n} & \mathbf{r}_a\times\mathbf{n} & -n &-\mathbf{r}_b\times\mathbf{n} \end{bmatrix} $$

注：Jacobian是我们最后应用不同物体冲量的方向例如

a->ApplyImpulseLinear(Vec2(Jacobian[0]*lambda, Jacobian[1]*lambda)); 
a->ApplyImpulseAngular(Jacobian[2]*lambda);                   
b->ApplyImpulseLinear(Vec2(Jacobian[3]*lambda, Jacobian[4]*lambda)); b->ApplyImpulseAngular(Jacobian[5]*lambda);           

求解冲量大小

根据我们的《物理引擎中的约束》最后的得到的方程我们可以解出冲量

$$ \lambda = -(JM^{-1}J^{T})^{-1}(JV) $$

带bias系数的形式

$$ \lambda = -(JM^{-1}J^{T})^{-1}(JV+b) $$

其中V为

$$ V=\begin{bmatrix} v_{ax} \\ v_{ay}\\ \omega_a\\ v_{bx} \\ v_{by} \\ \omega_b \end{bmatrix} $$

M的逆为

$$ M^{-1} = \begin{bmatrix} \frac{1}{m_a} & & & & & \\ & \frac{1}{m_a} & & & & \\ & & \frac{1}{I_a} & & & \\ & & & \frac{1}{m_b} & & \\ & & & & \frac{1}{m_b} & \\ & & & & &\frac{1}{I_b} \end{bmatrix} $$

JV是一个数，$JM^{-1}J^{T}$也是一个数，所以求出来$\lambda$也是一个数我们的公式是正确的

注:这里可以使用高斯-赛德尔（Gauss-Seidel）方法求解线性方程组