​ 在碰撞检测中如何检测两个物体是否相交？这里就介绍一种算法分离轴算法（SAT）。分离轴算法很好理解：如果两个物体彼此分离，那么一定能找到一条（只需要一条）轴线将这两个物体分隔在轴线的两侧，如图。

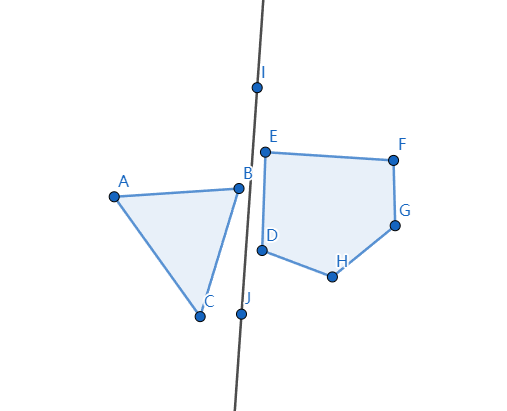
相反如果两个物体相交，那么一定找不到一条（只需要一条）轴线能将两个物体分隔在轴线的两侧。

​ 算法的原理就是这样，那么我们应该怎么将其翻译成代码呢？先仔细分析这个问题。注意到两个分离的物体在垂直于分离轴的直线上的投影是不相交的如图。

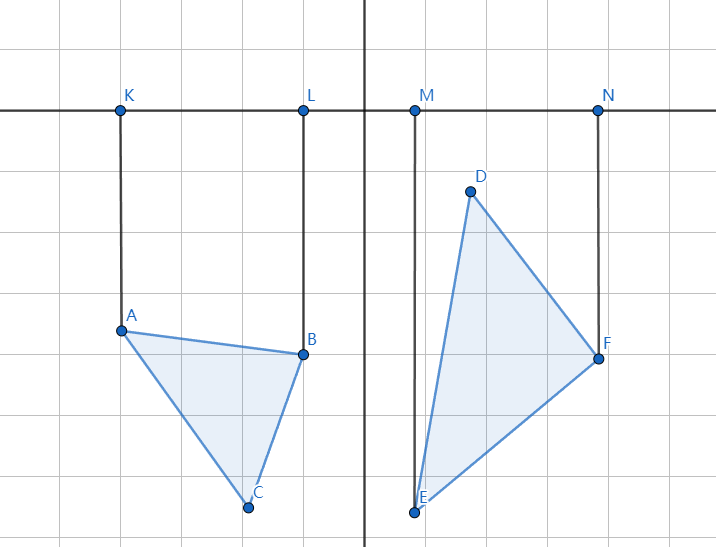
那么我们就将问题转为为如何找到一条轴使得两个物体在轴上的投影区间没有交集，事实上如果两个物体分离那么分离轴有无数条，我们只需找到一条就行，那么找轴的方式就有很多种。不妨我们将多边形的边作为轴，我们遍历多边形的每一条边，如果存在一条轴使得两个物体在轴上的投影区间没有交集那么我们就知道这两个物体没有发生碰撞。如图

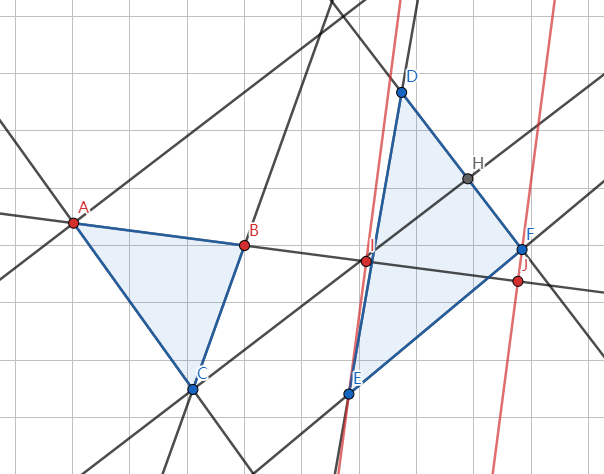
可以看到在三角形ABC以AB边为轴做两个物体的投影，[A,B],[I,J]观察可知区间[A,B],[I,J]无交集。事实上，判断两个区间是否有交集可以用以下算法

#include <iostream>
using namespace std;

//闭区间
struct Interval{
    float min_value;
    float max_value;
};

bool IntersectionIntervals(Interval& a,Interval &b){
    // 检查是否有交集
    if (a.min_value <= b.max_value && a.max_value >= b.min_value) {
        return true;  // 存在交集
    }
    return false;  // 不存在交集

}
int main(){
    Interval AB = {1,4};
    Interval IJ = {4,8};
    if(IntersectionIntervals(AB,IJ)){
        cout<<"存在交集";
    }
    else{
        cout<<"不纯在交集";
    }
    
    return 0;
}

​ 实际上，SAT算法只能用于判断凸多边形之间的碰撞，与凸多边形与圆形的碰撞，圆有一条特殊的轴，它由圆心与 离圆最近的多边形上的点连接而成。分析办法与多边形之间的碰撞类似。而其他非多边形不能使用SAT算法处理。

static IntersectData IntersectPolygons(const FlatVector& mass_center_a, const std::vector<FlatVector>& vertices_a,
    const FlatVector& mass_center_b, const std::vector<FlatVector>& vertices_b) {
    IntersectData data;
    data.depth = std::numeric_limits<float>::max();

    auto CheckAxis = [&](const FlatVector& axis, const std::vector<FlatVector>& vertices_a, const std::vector<FlatVector>& vertices_b) {
        // 计算多边形在该轴上的投影
        FlatVector project_polygon_a = ProjectVertices(axis, vertices_a);
        FlatVector project_polygon_b = ProjectVertices(axis, vertices_b);

        // 判断投影是否重叠
        if (project_polygon_a.y < project_polygon_b.x || project_polygon_b.y < project_polygon_a.x) {
            
            return false;
        }

        // 计算投影的重叠深度
        float axis_depth = std::min(project_polygon_b.y - project_polygon_a.x, project_polygon_a.y - project_polygon_b.x);     

        // 如果深度小于当前最小深度，则更新法向量和深度
        if (axis_depth < data.depth) {
            data.depth = axis_depth;
            data.normal = axis;
        }
        return true;
        };

    // 遍历多边形A的每条边
    for (int i = 0; i < vertices_a.size(); i++) {
        FlatVector v_a = vertices_a[i];
        FlatVector v_b = vertices_a[(i + 1) % vertices_a.size()];

        // 计算边的法向量
        FlatVector edge_vector = v_b - v_a;
        FlatVector axis;

        //保持法向量都指向图形外面
        if (edge_vector.x * edge_vector.y > 0) {
            axis = FlatVector(edge_vector.y, -edge_vector.x);
        }
        else if (edge_vector.x * edge_vector.y < 0) {
            axis = FlatVector(-edge_vector.y, edge_vector.x);
        }
        else {
            axis = FlatVector(edge_vector.y, -edge_vector.x);
        }
        axis.normalize();

        if (!CheckAxis(axis, vertices_a, vertices_b)) {
            
            return data; // 没有重叠，返回
        }
    }

    // 遍历多边形B的每条边
    for (int i = 0; i < vertices_b.size(); i++) {
        FlatVector v_a = vertices_b[i];
        FlatVector v_b = vertices_b[(i + 1) % vertices_b.size()];

        // 计算边的法向量
        FlatVector edge_vector = v_b - v_a;
        FlatVector axis;

        //保持法向量都指向图形外面
        if (edge_vector.x * edge_vector.y >0) {
             axis = FlatVector(edge_vector.y, -edge_vector.x);
        }
        else if (edge_vector.x * edge_vector.y < 0) {
             axis = FlatVector(-edge_vector.y, edge_vector.x);
        }
        else {
            axis = FlatVector(edge_vector.y, -edge_vector.x);
        }
        
        axis.normalize();

        if (!CheckAxis(axis, vertices_b, vertices_a)) {
           
            return data; // 没有重叠，返回
        }
    }