欧姆定律

通过某段导体的电流和这段导体两端电压成正比，跟它的电阻成反比（适用于纯电阻电路）

$$ R=\frac{U}{I} $$

数电压法

电流通过用电器时会导致电压降，经过电源时会导致电压升(其实没有这个概念)

单的说，负载两端的电势差就可以认为是电压降，电压降是电流流动的推动力。如果没有电压降，也就不存在电流的流动。

1

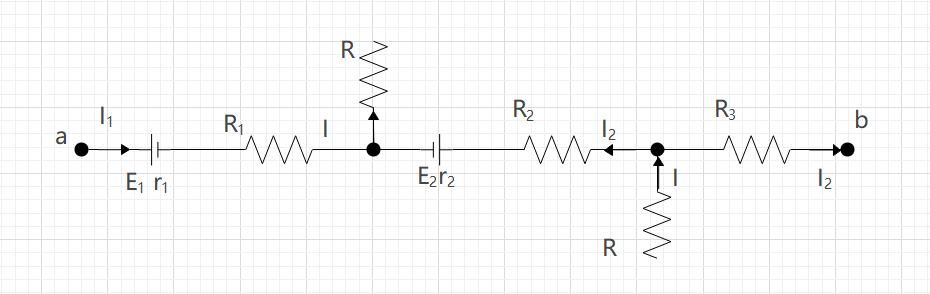
求ab两端的电压也就是求ab的电势差U ab可通过数电压法计算

当数电压方向与电流方向一致时电势降低为正号，电势升高为负号。当数电压方向与电流方向相反时电势降低为负号，电势升高为正号。

$$ U_{ab}=I_1(r_1+R_1)+E_1-I_2(R_2+r_2)-E_2+I_3R_3 $$

基尔霍夫定律

  1. 基尔霍夫第一定律（KCL）：是电路中任一个节点上，在任一时刻，流入节点的电流与流出节点的电流之和为零，一般选定流入为正流出为负。以方程表达，对于电路的任意节点满足：

    $$ \sum_{k=1}^{n} i_k=0 $$

    其中，ik是第 k 个进入或离开这节点的电流，是流过与这节点相连接的第 k 个支路的电流。

    例如

    2

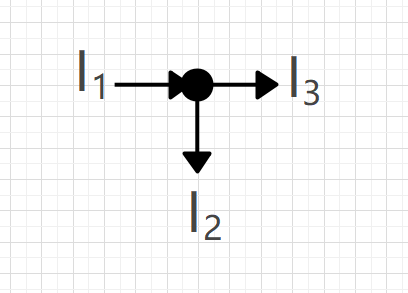
    $$ I_1=I_2+I_3 $$

    对于一个闭合回路可以看成一个大节点

    3

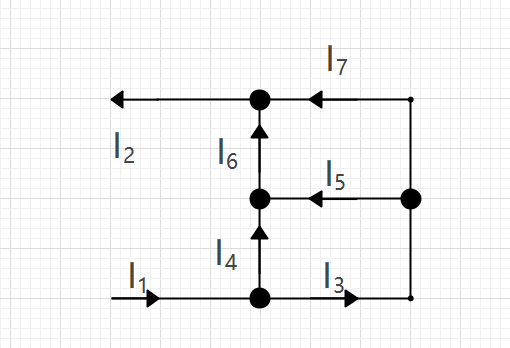
    $$ I_1=I_4+I_3① $$

    $$ I_6=I_5+I_4② $$

    $$ I_3=I_5+I_7③ $$

    $$ I_2=I_6+I_7④ $$

    联立①②③④得

    $$ I_1=I_2 $$

  2. 基尔霍夫第二定律（KVL）:沿着闭合回路所有元件两端的电势差（电压）的代数和等于零。以方程表达，对于电路任意回路满足：

    $$ \sum_{k=1}^{m} V_k=0 $$

    其中，m 是这闭合回路的元件数目， Vk是元件两端的电压.

    基尔霍夫电压定律不仅应用于闭合回路，也可以把它推广应用于回路的部分电路（后面会提到）

    • 应用

    在使用KVL时，先设定浏览整个电路的绕行方向，在看电流方向，如果在电流方向未知时可设出电流方向，电流满足KCL，解出方程后若电流的方向为正，则与设定的电流方向一致，若为负则此电流的方向与设定的电流方向相反。再沿绕行方向写电压，写电压规则与数电压法一致。

    4

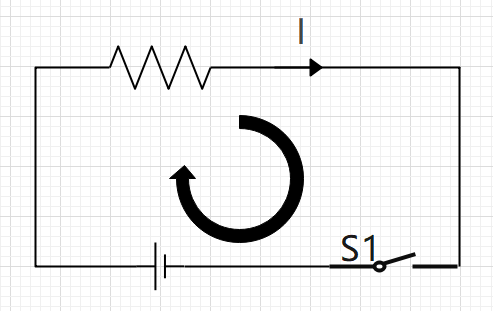
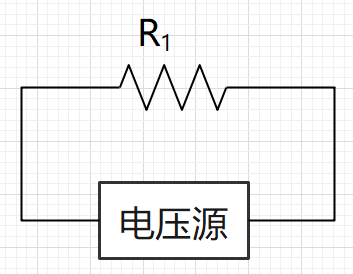
    列出KVL方程

    $$ IR+Ir-E=0 $$

    简化电路法

    要点：1）同一根导线上电势相等，2）把电流表看成一根导线，电压表看成断路。

    5

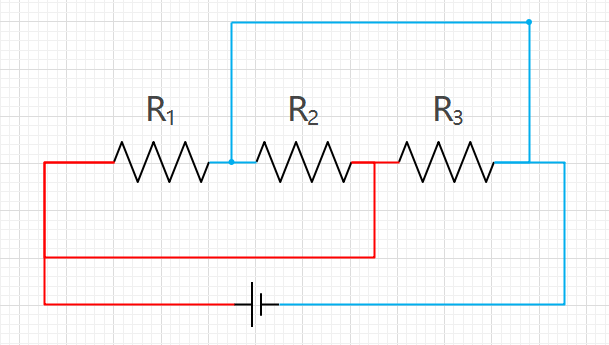
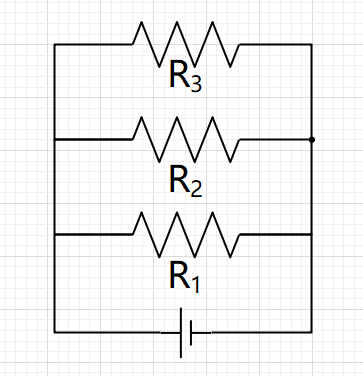
如图，红色都为同一根导线，蓝色也为同一根导线。所以设红导线上的电势为a，设蓝导线上的电势为b。则R1，R2，R3，电源两端的电势都相同。则它们4个并联

6

等效电源法

等效电压源定理（戴维宁定理）：

两端有源网络可以等效为一个电压源，其电动势等与网络开路时的路段电压，内阻等于网络从开路看除源（将电动势短路，内阻仍然保留在网络中）网络的电路。

7

8

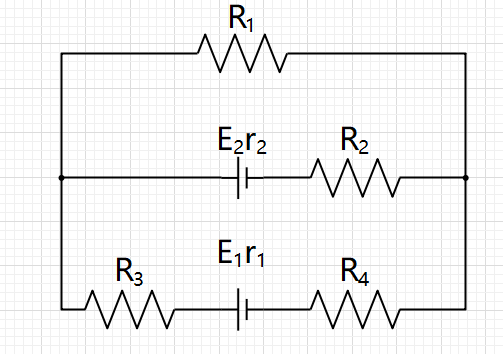
如图R1=10欧，R2=19欧，R3=4.5欧，R4=5欧，r1=0.5欧，r2=1欧，求通过R1的电流I

第一步把R1拿掉，第二步算电压源电动势与内阻，第三步简化电路，第四步计算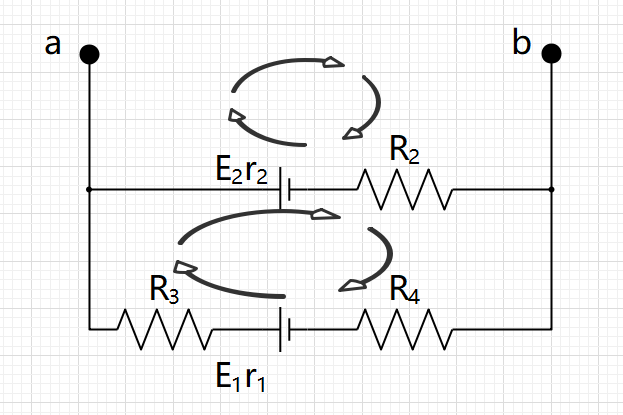9

Uab就是我们要求的等效电压源的电动势，设电流方向，这里设的是与下面那个绕行方向是一致的。写出KVL方程

$$ E_2+I(R_2+R_4+R_3+r_2+r_1)-E_1=0 $$

电路上方是个开路按理来说是不能用KVL的，但是断路那里有压降，且压降与下面的电路有关则还是可以用KVL的（其实有点强行解释若有知道正确解释的，请各位大佬在评论区指出）。

$$ U_{ab}-I(R_2+r_2)-E_2=0 $$

联立解得

$$ U_{ab}=\frac{7}{3}V $$

还有R0内阻

我们把图9中的电源看成一根导线，从开路方向看去

$$ R_0=\frac{(R_4+r_2)(R_3+r_1+R_2)}{R_4+r_2+R_3+r_1+R_2} $$

简化电路

10

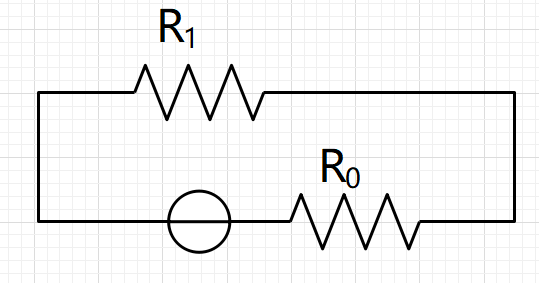
利用欧姆定律解得

$$ I=\frac{U_{ab}}{R_1+R_0}=0.14A $$

等效电流源定理（诺顿定理）：

两端有源网络可等效为一个电流源，电流源的电流等于网络两端断路时流经两端点的电流，内阻等于从网络两端看除源网络的电阻。

11

还是用图8那个例子。

第一步把R1拿掉并接上导线，第二步算电压源电动势与内阻，第三步简化电路，第四步计算

12

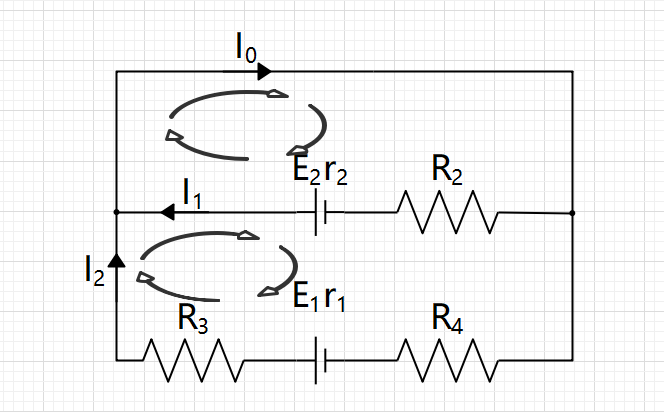
直接按照KVL列方程

$$ \left\{\begin{matrix}I_1R_2+I_1r_2-E_2=0 \\I_2(R_4+R_3+r_1)-E_1+E_2-I_1(R_2+r_2)=0 \\ I_0=I_1+I_2 \end{matrix}\right. $$

解得

$$ I_0=\frac{7}{20}A $$

电源看成一根导线，从短路方向看去

$$ R_0=\frac{(R_4+r_2)(R_3+r_1+R_2)}{R_4+r_2+R_3+r_1+R_2} $$

简化电路

13

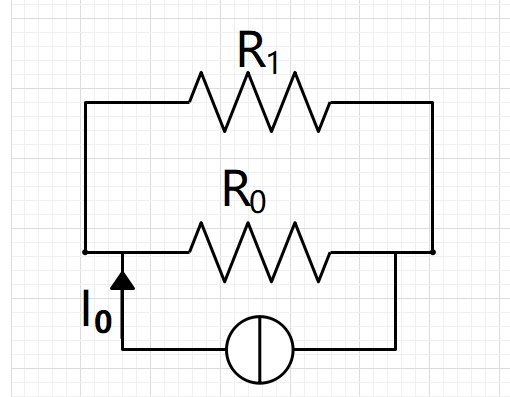
利用并联分流公式有

$$ I=I_0\frac{R_0}{R_0+R_1}=0.14A $$

叠加定理

若电路中有多个电源，则通过电路中任意一条支路的电流等于各个电动势单独存在时在该支路产生的电流之和

还是以图8为例，用叠加定理求R1电流I

根据叠加定理有

14

15

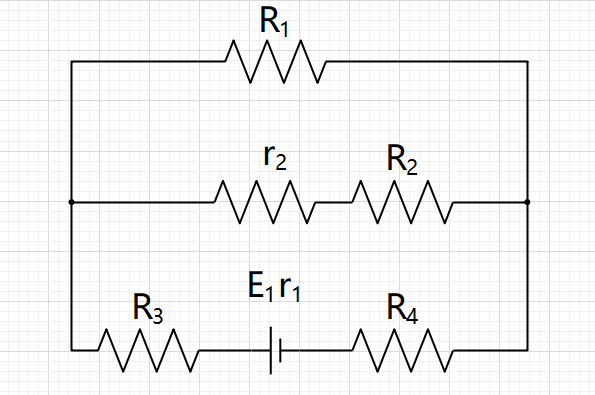
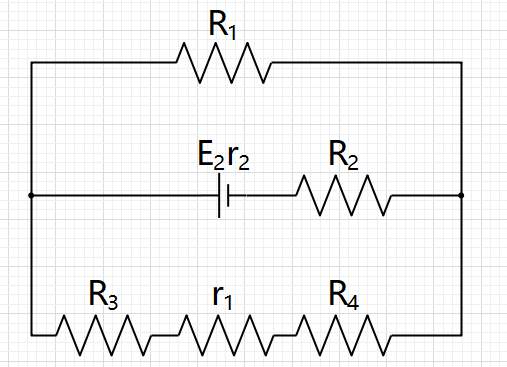
先对图14分析，设图14通过R1的电流为I1

$$ I_1=\frac{E_1\frac{r_2+R_2}{R_1+r_2+R_2}}{(r_1+R_4+R_3)+\frac{R_1(r_2+R_2)}{R_1+r_2+R_2}}=\frac{6}{50}A $$

对图15分析，设图15通过R1的电流为I2

$$ I_2=\frac{E_2\frac{R_3+r_1+R_4}{R_1+R_3+r_1+R_4}}{R_2+r_2+\frac{R_1(R_3+r_1+R_4)}{R_1+R_3+r_1+R_4}}=\frac{1}{50}A $$

再有

$$ I=I_1+I_2=0.14A $$

最后修改：2023 年 12 月 19 日
© 允许规范转载
如果觉得我的文章对你有用，请随意赞赏