在上一篇文章中我们使用了化简后的Rosenblatt感知器进行回归预测，在这篇文章中我们将了解损失函数、梯度下降算法以及梯度下降算法的的实现，且加入偏置项系数b。

损失函数

损失函数(Loss Function)：定义在单个样本上，算的是一个样本的误差.

代价函数(Cost Function)：定义在整个训练集上，算的是所有样本的误差，也就是损失函数的平均。

在机器学习中几乎所有的模型都会有损失函数，损失函数描述的是：

预测值和样本数据的实际目标值之间的误差与预测函数的系数之间的关系

均方误差

均方误差代价函数其表达式如下：

$$ e(w,b) = \frac{1}{n}\sum_{i=0}^{n}(y_{i}-(wx_{i}+b))^2 $$

其中y_i表示样本数据的实际目标值表示wx_i+b预测值根据样本数据x_i计算出的预测值。

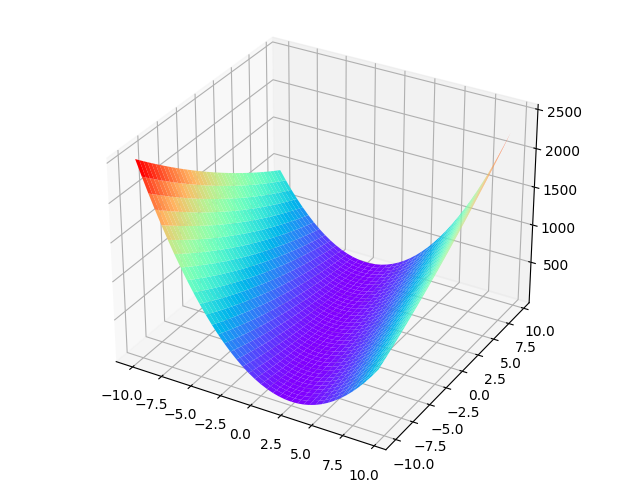
我们可以发现这个图像是一个开口向上的二元二次函数图像，既然是一个开口向上的二元二次函数，那么我们是不是可以找到一个w和b使得整体误差最小(全局最优解)呢？是的在机器学习中正是这样。

寻找最低点的方法有

• 正规方程

  $$ w=\frac{\sum_{i=0}^{n}(x_{i}y_{i})}{\sum_{i=0}^{n}x_{i}^2} $$

  推导过程是使用了二元一次函数的顶点坐标公式

• 梯度下降

梯度下降

梯度下降(Gradient descent)的可以类比为一个下山的过程，如图所示函数看似为一座山，山中全是雾，有一个人在山上任意一个位置想要快速找到水，由于山上全是雾，人只能看见脚下的路，那么人可以判断脚下土地的坡度判断自己是否为下坡路，每走一步调整自己的方向，每次向坡度最大的方向走，就走到最低点的位置喝到水。

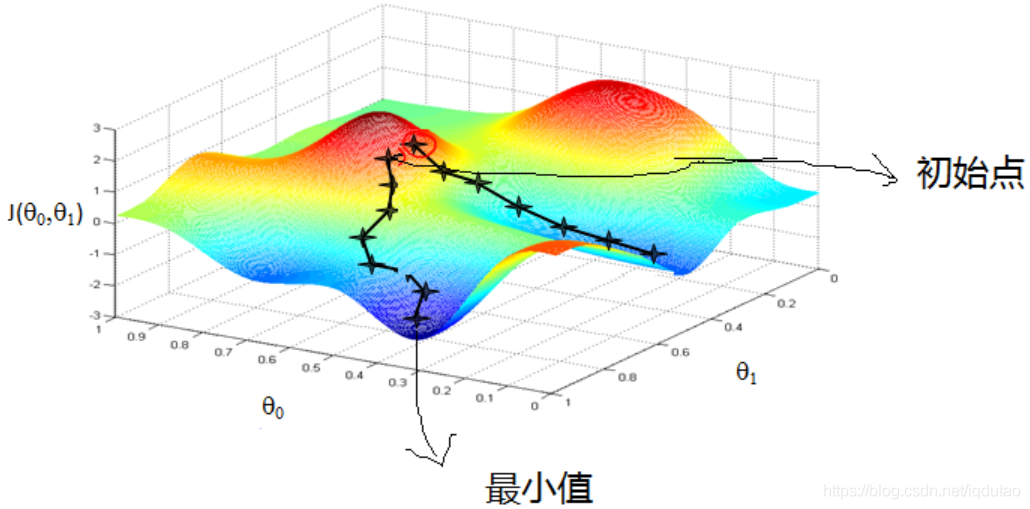
数学中实现

在数学中具有一个概念叫做梯度，梯度描述的就是一个面上某个点的瞬时变化率。和斜率类似，其实梯度就是斜率更广的说法。

既然描述的是面上某个点的瞬时变化率，那么我们就可以对他进行求导。我们要得到w最小同时b最小的一个点，我们只需要分别对w和b求偏导，当某个点的梯度大于零，对应的偏导数大于零我们只需要让对应的值减去alpha(alpha>0)倍的偏导数，偏导数为正，对应值往小的调整；当某个点的梯度小于零，对应的偏导数小于零我们只需要让对应的值减去alpha(alpha>0)倍的偏导数，偏导数为负，对应值往大的调整。

• 为什么要在偏导数上乘以一个alpha

  alpha叫做学习率，在上一篇文章中遇到过。在调整w和b的过程中如果没有学习率alpha它将可能无法或者很慢的回到最低点，乘以一个alpha可以加快或者调慢速度

$$ \xi =\xi -\alpha \times \frac{\partial f(\xi )}{\partial \xi } $$

随机梯度下降算法

随机梯度下降算法(SGD)取出其中一个样本的数据依次进行梯度下降

反向传播

我们已经知道了梯度下降算法，但是我们如何获得求得损失函数中w和b的偏导呢。其实高中数学足以

观察公式：

$$ e(w,b) = (y_{i}-(wx_{i}+b))^2 $$

使用复合函数的求导法则：

$$ \frac{\partial e}{\partial w}=2(y_{i}-b-wx_{i})\cdot (-x_{i}) $$

$$ \frac{\partial e}{\partial b}=2(y_{i}-b-wx_{i})\cdot (-1) $$

调整w和b

$$ w =w -\alpha \times \frac{\partial e}{\partial w } $$

$$ b =b -\alpha \times \frac{\partial e}{\partial b } $$

代码实现

将使用SGD实现

首先先引入需要用到的库

import numpy
from matplotlib import pyplot as plt

引入numpy数学库以方便我们的数学计算

引入matplotlib中的pyplot模块进行画图操作

生成数据以便进行训练

def getdata(count):
    """获取指定数量的数据"""
    x = np.random.rand(count)  # 生成区间[0,1)的随机数
    x = np.sort(x)  # 进行从小到大排序
    y = [-1.5*xx+np.random.rand()/3+1 for xx in x]  # 使用列表推导式生成对应的值
    return x, y

创建一个名为getdata的函数随机生成有共同特征的数据，有一个参数count来接收获取数据的数量

获取100个数据

data = getdata(100)
xs = data[0]
ys = data[1]

编写预测函数

w = np.random.rand(1)
b = np.random.rand(1)
z = w*xs+b

绘制图像

plt.xlim(0, 1)
plt.ylim(0, 3)
plt.scatter(xs, ys)
plt.plot(xs, z)
plt.show()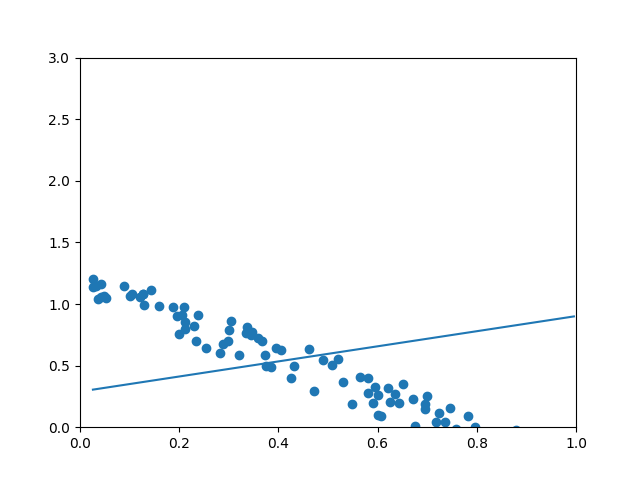

随机梯度下降算法和反向传播

for j in range(500):
    for i in range(len(xs)):
        x = xs[i]
        y = ys[i]

        z = w*x+b
        e = (y - z)**2#损失函数
        alpha = 0.05
        
        #反向传播和随机梯度下降
        dedz = -2*(y-z)
        dzdw = x
        dzdb = 1
        dedw = dedz*dzdw
        w = w - alpha*dedw
        dedb = dedz*dzdb
        b = b - alpha*dedb
        
        """
        你也可以这么写
        dedw = -2*(y-z)*x
        w = w - alpha*dedw
        dedb = -2*(y-z)*1
        b = b - alpha*dedb
        """

再次绘制拟合后的图像

z = w*xs+b
plt.xlim(0, 1)
plt.ylim(0, 3)
plt.scatter(xs, ys)
plt.plot(xs, z)
plt.show()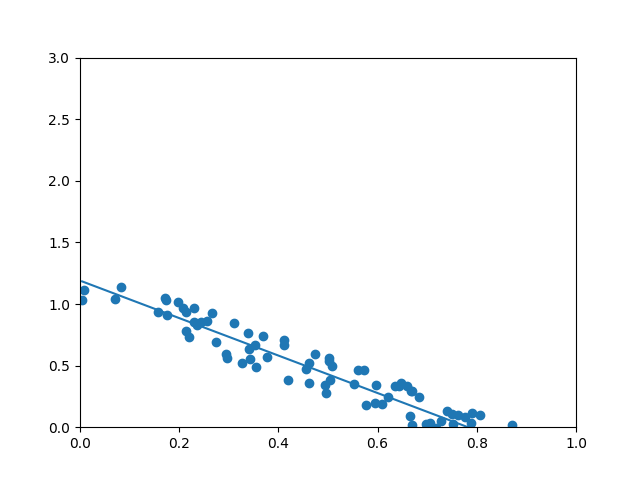

可以看到已经完美拟合

完整代码

# 导入numpy库
import numpy as np
from matplotlib import pyplot as plt


def getdata(count):
    """获取指定数量的数据"""
    x = np.random.rand(count)  # 生成区间[0,1)的随机数
    x = np.sort(x)  # 进行从小到大排序
    y = [-1.5*xx+np.random.rand()/3+1 for xx in x]  # 使用列表推导式生成对应的值
    return x, y


data = getdata(100)
xs = data[0]
ys = data[1]

w = np.random.rand(1)
b = np.random.rand(1)
z = w*xs+b

plt.xlim(0, 1)
plt.ylim(0, 3)
plt.scatter(xs, ys)
plt.plot(xs, z)
plt.show()

for j in range(500):
    for i in range(len(xs)):
        x = xs[i]
        y = ys[i]

        z = w*x+b
        e = (y - z)**2
        alpha = 0.05

        dedz = -2*(y-z)
        dzdw = x
        dzdb = 1

        dedw = dedz*dzdw
        w = w - alpha*dedw
        dedb = dedz*dzdb
        b = b - alpha*dedb
        """
        你也可以这么写
        dedw = -2*(y-z)*x
        w = w - alpha*dedw
        dedb = -2*(y-z)*1
        b = b - alpha*dedb
        """

z = w*xs+b
plt.xlim(0, 1)
plt.ylim(0, 3)
plt.scatter(xs, ys)
plt.plot(xs, z)
plt.show()