光栅化 | Rasterization

光栅化是计算机图形学中将矢量几何图形（如三角形、多边形）转换为栅格图像（像素）的核心过程，广泛应用于实时渲染（如游戏）。

现代光栅化的基本流程如下

顶点处理：通过顶点着色器处理3D模型的顶点坐标（模型空间→世界空间→视图空间→用户空间）。
图元组装：将顶点连接成图元（如三角形、线段）。
裁剪与透视除法：剔除视锥外的图元，将坐标转换到屏幕空间。
扫描转换：确定图元覆盖的像素（如判断像素中心是否在三角形内）。
插值：对颜色、纹理坐标、深度等属性进行插值（常用重心坐标）。
像素处理：执行片段着色器(像素着色器)计算颜色，处理深度测试、抗锯齿等。
输出到帧缓冲：最终像素写入帧缓冲区，显示到屏幕。

光栅化设备

光栅化设备（Rasterization Device） 是将矢量图形或几何数据转换为栅格图像（即像素阵列）的硬件或系统。这类设备的核心任务是通过光栅化算法，将连续的几何形状（如点、线、三角形）离散化为离散的像素，以便在数字显示设备（如屏幕、打印机）上呈现。

顶点处理、裁剪与透视除法

在上一篇文章中已经介绍过了

图元组装与扫描转换

直线的光栅化算法

处理线段的图元组装算法主要有三中，分别是DDA算法，BRESENHAM算法，中点画线法，这里不过多介绍，有兴趣的可以去该链接学习[[1]](https://zhuanlan.zhihu.com/p/20213658)

三角形的光栅化算法

思考一下问题，我们如何在已知三角形顶点属性的情况下在光栅化设备上绘制一个实心的三角形？那么我们就得知道哪些点在三角形内哪些点在外。那么问题就被转化为在已知三角形的顶点属性的条件下，如何判断任意点（像素）是否在三角形内。

我们根据二维向量叉乘的性质

$$ 如果\overrightarrow{OA} \times \overrightarrow{OB}>0，则\overrightarrow{OB}在\overrightarrow{OA}逆时针旋转方向上\\如果\overrightarrow{OA} \times \overrightarrow{OB}<0，则\overrightarrow{OB}在\overrightarrow{OA}顺时针旋转方向上\\如果\overrightarrow{OA} \times \overrightarrow{OB}=0，则\overrightarrow{OB}与\overrightarrow{OA}共线 $$

如果我们以逆时针方向遍历三角形ABC的顶点，并且判断点P是否在三角形内，如果需要满足

$$ \overrightarrow{AB} \times \overrightarrow{AP}>0\\ \overrightarrow{BC} \times \overrightarrow{BP}>0\\ \overrightarrow{CA} \times \overrightarrow{CP}>0\\ $$

则该点在三角形内

如果以顺时针方向遍历三角形ABC的顶点，则需要满足

$$ \overrightarrow{AC} \times \overrightarrow{AP}<0\\ \overrightarrow{CB} \times \overrightarrow{CP}<0\\ \overrightarrow{BA} \times \overrightarrow{BP}<0\\ $$

根据这个性质我们编写一个inside(Triangle,Point)函数，判断点是否在三角形内

包围盒 | Bounding Box

如果对可使范围类所有的点都进行一次inside(Triangle,Point)判断，那么将会浪费大量计算资源，为了解决这个问题我们使用包围盒减少需要判断的点。

包围盒是个矩形，它会将三角形包围起来，其中右上角点为(Triangle(max(x)),Triangle(max(y)))，左下角点为(Triangle(min(x)),Triangle(min(y)))，现在只需要判断包围盒中点的是否在三角形内即可。

插值

这里先讲一下颜色插值，由于纹理，深度还不会。

使用重心坐标插值

重心坐标并不是重心的坐标，在三角形内部的每个点都有一个重心坐标。

对于三角形内部每个点的重心坐标计算如下（图片来源于games101）

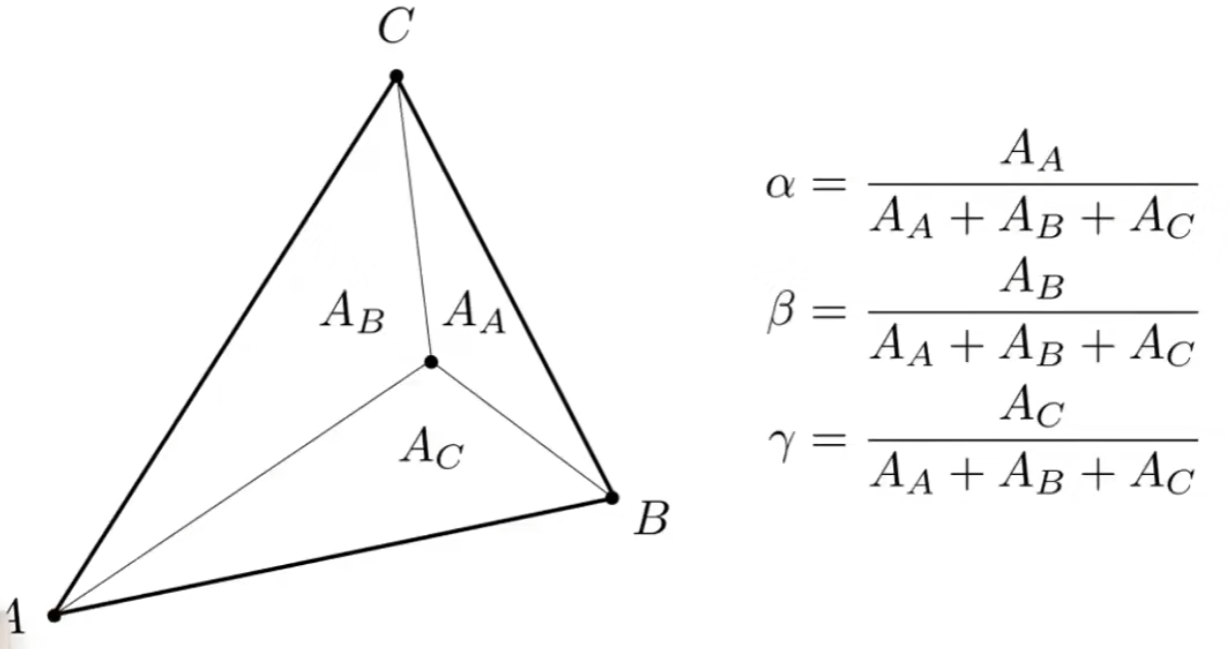
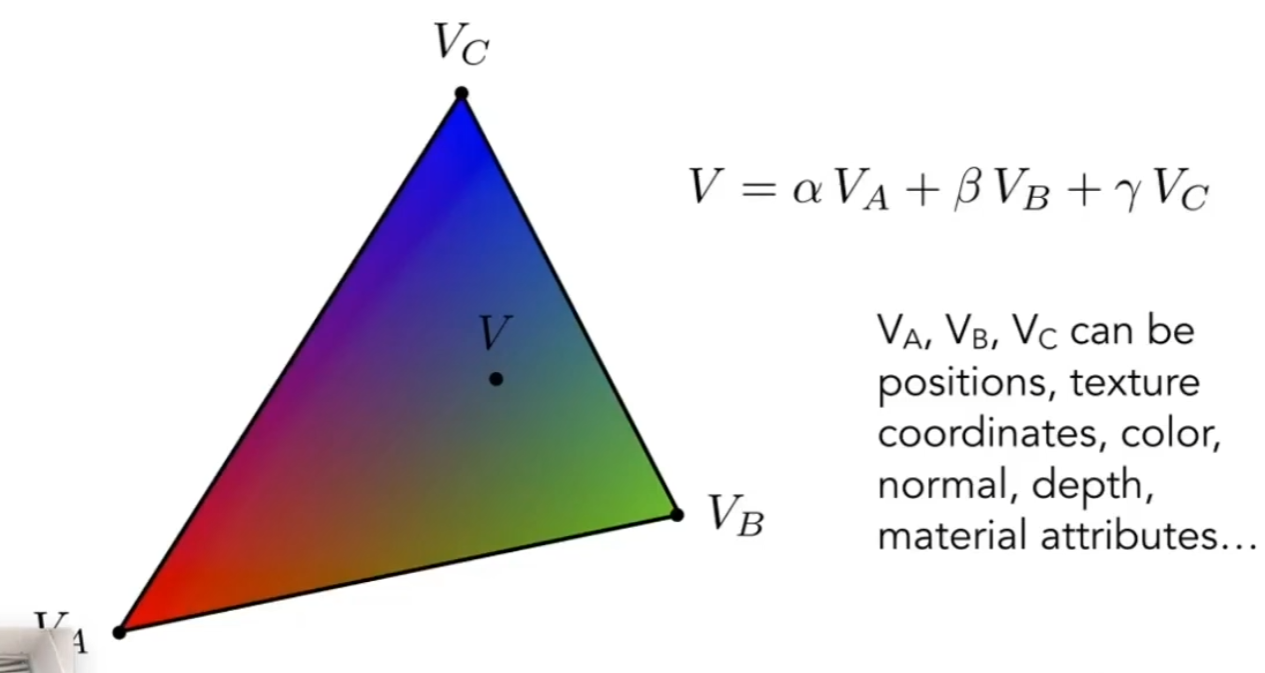
auto sign = [](oeVec2 p1, oeVec2 p2, oeVec2 p3) {
            return (p1.x - p3.x) * (p2.y - p3.y) - (p2.x - p3.x) * (p1.y - p3.y);};

double A_C = sign(P, to_vec2(vertex1), to_vec2(vertex2));
double A_A = sign(P, to_vec2(vertex2), to_vec2(vertex3));
double A_B = sign(P, to_vec2(vertex3), to_vec2(vertex1));

// 判断分母符号，确保面积比例正确
if (S_Triangle < 0) {
    S_Triangle = -S_Triangle;
    A_C = -A_C;
    A_A = -A_A;
    A_B = -A_B;
}
double alpha = A_A / S_Triangle;
double beta = A_B / S_Triangle;
double gamma = A_C / S_Triangle;

if (u >= 0 && u <= 1 && v >= 0 && v <= 1 && w >= 0 && w <= 1) {
int red = static_cast<int>(alpha * r1 + beta * r2 + gamma * r3);
int green = static_cast<int>(alpha * g1 + beta * g2 + gamma * g3);
int blue = static_cast<int>(alpha * b1 + beta* b2 + gamma * b3);

像素处理

MSAA抗锯齿

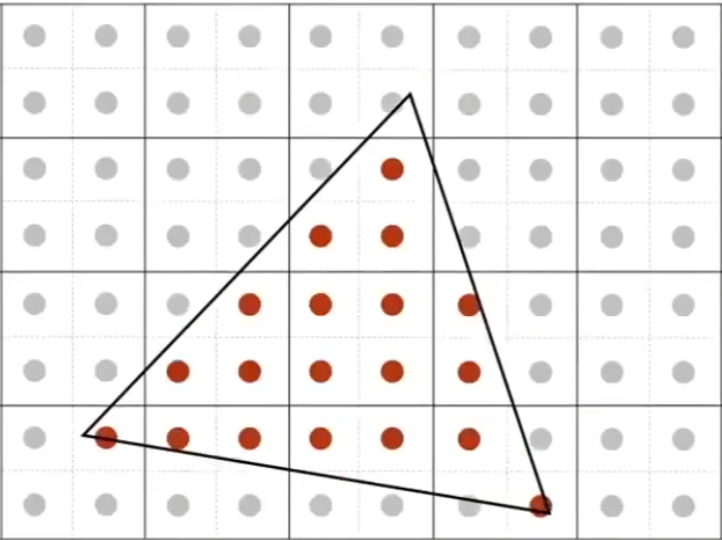
对每个像素虚构出来一些子像素，即对像素再进一步划分。如对一个像素划分成一个由2*2的子像素组成，那么对每个像素的子像素进行inside测试，如果该像素不在三角形内但是存在一些子像素在三角形内，则可根据子像素在三角形内的个数的比例对该像素进行上色。

Z-Buffer（深度缓冲）

是计算机图形学中用于解决三维物体遮挡关系的核心技术，属于光栅化渲染管线中的关键环节。它通过记录每个像素的深度值（即物体到摄像机的距离），决定哪些片段（Fragment）最终可见，从而实现三维场景的正确渲染。

深度值存储：
Z-Buffer是一个与屏幕像素一一对应的二维数组（即缓冲区），每个元素存储对应像素的当前最小深度值（通常用浮点数表示）。
- 深度值范围：一般归一化为 [0, 1]，0代表近裁剪面（Near Clip Plane），1代表远裁剪面（Far Clip Plane）。
- 坐标系：在透视投影中，深度值是非线性分布的（近处精度高，远处精度低）。
深度测试（Depth Test）：
在渲染每个片段（像素候选）时，系统会执行以下操作：
1. 计算当前片段的深度值（基于顶点插值或透视校正插值）。
2. 将其与Z-Buffer中同一位置的现有深度值比较。
3. 若当前片段更近（深度值更小）：更新颜色缓冲（Color Buffer）和Z-Buffer；
  否则：丢弃该片段（被遮挡）。
以渲染一个三角形为例：
1. 顶点处理：将三角形的顶点转换到屏幕空间，计算各顶点的深度值。
2. 光栅化：生成覆盖的像素（片段），并通过插值得到每个片段的深度值。
3. 深度测试：对每个片段，与Z-Buffer中的值比较：
  - 若通过测试（更近），则写入颜色和深度值；
  - 若未通过，则丢弃。
4. 最终输出：所有片段处理完成后，颜色缓冲即为渲染结果。