线性映射与线性变换
线性映射
$$ \begin{array}{c} 若存在向量空间若存在两个向量空间 V和 W\\一个函数 T:V→W若满足:\\ 加法性:T(u+v)= T(u)+T(v),对所有的u,c\in V\\ 齐次性:T(cu) = cT(u),对所有标量c和u\in V\\ 则称T为线性映射 \end{array} $$
线性变换
$$ \begin{array}{c} 当线性映射的定义域与到达域为同一个向量空间时,即T:V→V\\ ,称其为 线性变换。它是线性映射的特例 \end{array} $$
矩阵的线性性
我们类比发现矩阵乘法满足线性映射的条件,所以自然可以用矩阵对图形进行线性变换
模型变换 | Model Transformation
对于二维图形
缩放变换 | Scaling
$$ \begin{array}{c} scale(s_x,s_y)=\begin{bmatrix} s_x & 0\\ 0&s_y \end{bmatrix} \end{array} $$
示例1
$$ \begin{array}{c} scale(0.5,0.5)=\begin{bmatrix} 0.5 & 0\\ 0&0.5 \end{bmatrix} \end{array} $$
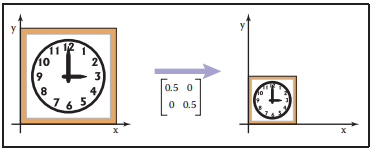
示例2
$$ \begin{array}{c} scale(0.5,0.5)=\begin{bmatrix} 0.5 & 0\\ 0&1.5 \end{bmatrix} \end{array} $$
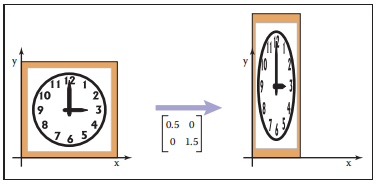
剪切变换 | Shearing
$$ \begin{array}{c} shear_x(s)=\begin{bmatrix} 1 & s\\ 0&1 \end{bmatrix},shear_y(s)=\begin{bmatrix} 1 & 0\\ s&1 \end{bmatrix} \end{array} $$
示例
$$ shear_x(1)=\begin{bmatrix} 1 & 1\\ 0&1 \end{bmatrix} $$
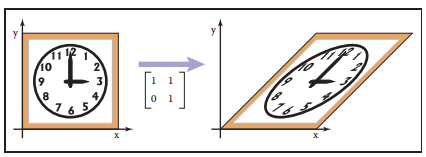
旋转变换 | Rotation
$$ rotate(\phi) = \begin{bmatrix} \cos \phi & -\sin \phi \\ \sin \phi &\cos \phi \end{bmatrix} $$
注:旋转是逆时针旋转
示例
$$ rotate(\frac{\pi}{4}) = \begin{bmatrix} \cos \frac{\pi}{4}& -\sin \frac{\pi}{4} \\ \sin \frac{\pi}{4} &\cos \frac{\pi}{4} \end{bmatrix} = \begin{bmatrix} 0.707 &-0.707 \\ 0.707&0.707 \end{bmatrix} $$
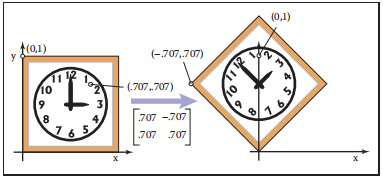
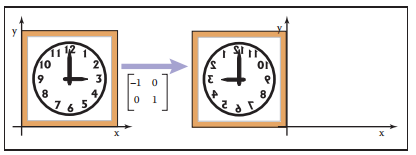
反射变换 | Reflection
$$ reflect_y = \begin{bmatrix} -1 & 0 \\ 0 &1 \end{bmatrix},reflect_x = \begin{bmatrix} 1 & 0 \\ 0 &-1 \end{bmatrix} $$
示例
三维变换
缩放变换
$$ scale(s_x,s_y,s_z) =\begin{bmatrix} s_x & 0&0 \\ 0& s_y&0 \\ 0& 0 &s_z \end{bmatrix} $$
旋转变换
绕z轴旋转
$$ rotate_z(\phi ) =\begin{bmatrix} \cos \phi & -\sin \phi&0 \\ \sin \phi& \cos \phi&0 \\ 0& 0 &1\end{bmatrix} $$
绕x轴旋转
$$ rotate_x(\phi ) =\begin{bmatrix} 1& 0 &0\\ 0& \cos \phi&-\sin \phi \\ 0&\sin \phi& \cos \phi \end{bmatrix} $$
绕y轴旋转
$$ rotate_y(\phi ) =\begin{bmatrix} \cos \phi& 0 &\sin \phi\\ 0& 1& 0\\ -\sin \phi&0& \cos \phi \end{bmatrix} $$
平移和仿射变换 | Translation and Affine Transformations
线性变换有个局限性,只能旋转和缩放对象。要移动对象的点就需要进行一下变换。
$$ \begin{matrix} x' =x+x_t \\ y'=y+y_t \end{matrix} $$
通过将(x,y)乘以2*2的矩阵无法做到这一点。但是为了将形式(线性变换)统一我们将原变换矩阵写成
$$ T' = \begin{bmatrix} T & 0\\ 0 &1 \end{bmatrix} $$
再定义平移矩阵为
$$ \begin{array}{c} Translation(\alpha ) = \begin{bmatrix} 1 & \alpha\\ 0 &1 \end{bmatrix},其中\alpha ^T = [a,b,...,k]\\特别的对于三维坐标下\\ Translation(x_s,y_s,z_s) = \begin{bmatrix} 1 & 0& 0& x_s\\ 0& 1 & 0& y_s\\ 0& 0 & 1 & z_s\\ 0& 0 & 0&1 \end{bmatrix}其中x_s,y_s,y_s是在其xyz轴上的平移量 \end{array} $$
那么对于一个放射变换
$$ \\如对三维坐标系下的点(x,y,z,1)绕z轴旋转45度再平移(1,1,1)则可以写成 $$
$$ \begin{array}{c} \begin{bmatrix} 1 & 0&0 & 1\\ 0& 1& 0 & 1\\ 0& 0 & 1& 1\\ 0&0 & 0&1 \end{bmatrix}\begin{bmatrix} \cos \frac{\pi}{4}& -\cos \frac{\pi}{4} & 0& 0\\ \cos \frac{\pi}{4}& \cos \frac{\pi}{4} & 0 & 0\\ 0 & 0 &1 & 0\\ 0& 0 & 0 &1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} = \begin{bmatrix} \cos \frac{\pi}{4}& -\cos \frac{\pi}{4} & 0& 1\\ \cos \frac{\pi}{4}& \cos \frac{\pi}{4} & 0 & 1\\ 0 & 0 &1 & 1\\ 0& 0 & 0 &1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} \end{array} $$
坐标变换
坐标变换可以看作是将坐标系的基底向量的放射变换。
$$ \begin{array}{c} 设A坐标系是以\hat{x} \hat{y}\hat{z}为基底向量,B坐标系是以\hat{u}\hat{v}\hat{w}为基底向量\\那么将B中的坐标变换到A中去我们需要做的就是将B的基底向量\\变换成A的基底向量使得\\ \hat{x}=\hat{u}\\ \hat{y}=\hat{v}\\ \hat{z}=\hat{w} \end{array}\\ $$
实现这一过程需要一个矩阵,这个矩阵就是左边变换矩阵
$$ \begin{array}{c} A = \begin{bmatrix} u & v & w &e \\ 0 & 0 & 0&1 \end{bmatrix}B \end{array}\\ $$
视图变换 | Viewing Transformations
想想我们是怎么拍一张照片的
- 模型/人物摆好pose(模型变换)
- 摆好相机,确定相机的位置(视图变换)
- 拍照(投影变换)
定义一个相机
- position(相机在哪)e
- look-at/gaze direction(朝哪个方向)g
- up direction(向上方向:控制歪斜)t
同时,相机默认的向上方向为+Y。永远朝着-Z方向看,永远在原点上。
将任意相机变换到到默认方式上去。
- 将相机位置平移到默认点上去即原点
- 将相机的up direction旋转到+y轴上去
- 将相机的look at旋转到-z上去
- 另一个轴即g叉乘t自然被旋转到x轴上去了
正交投影 | Orthogonal projection
正交变换的目标是将物体从视图空间(相机坐标系)映射到规范化设备坐标系(NDC)。以下是关键点的分步解释:
- 世界坐标系:所有物体的初始位置和方向均定义在此坐标系下。
- 相机坐标系:通过视图变换(View Transform),将世界坐标系中的物体转换到以相机为原点的坐标系。此时,相机看向 -z 轴方向,位于原点。
- 规范化设备坐标系(NDC):通过投影变换(包括正交投影),将视景体内的物体映射到 [-1,1]³ 或 [0,1]³ 的立方体中。
2. 正交投影的核心步骤
平移与缩放视景体:正交投影矩阵的作用是将视景体(如长方体 [left, right] × [bottom, top] × [near, far])平移到原点并缩放到规范化范围。例如:
- 平移矩阵将视景体中心移至原点。
- 缩放矩阵将视景体的宽度、高度、深度分别缩放到 2 个单位(如从 -1 到 1)。
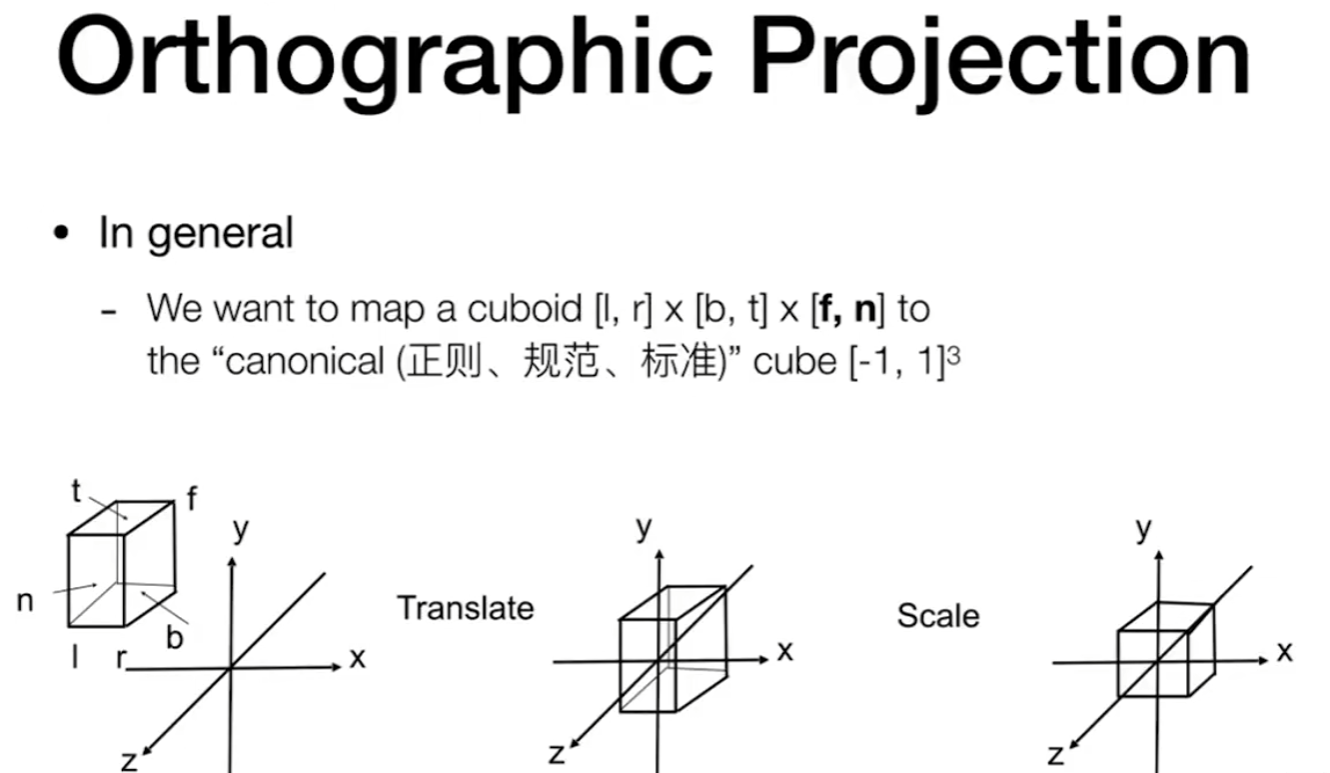
通过上述变换我们可以得到正交变换矩阵
$$ M_{ortho}=\begin{bmatrix} \frac{2}{r-l} &0 & 0& 0\\ 0 & \frac{2}{t-b} & 0 &0 \\ 0 & 0 & \frac{2}{n-f} &0 \\ 0 & 0 & 0 &1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0&-\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 &0 & 1 & -\frac{n+f}{2}\\ 0&0 & 0&1 \end{bmatrix} $$
透视投影 | Perspective projection
在计算机图形学中,透视投影(Perspective Projection)是一种模拟人眼视觉效果的投影方式,能够实现“近大远小”的透视效果。它与正交投影的核心区别在于:透视投影考虑了深度对物体尺寸的影响,而正交投影仅保留平行关系,不改变物体大小。
1. 透视投影的核心目标
将三维物体从视锥体(Frustum)(相机坐标系中的平截头体空间)映射到规范化设备坐标系(NDC)([-1,1]³ 或 [0,1]³ 的立方体)。
关键步骤包括:
- 压缩视锥体为立方体(通过投影矩阵)。
- 透视除法(齐次坐标的归一化)。
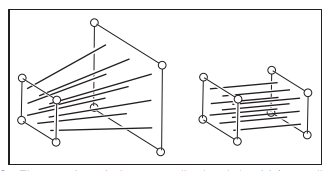
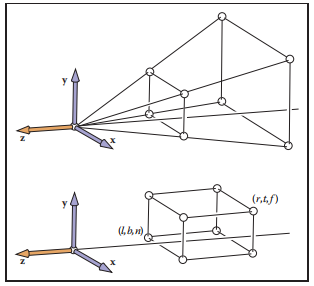
2. 视锥体的定义
视锥体是一个被近平面(Near Plane)和远平面(Far Plane)截断的金字塔形空间,由以下参数定义:
- 垂直视场角(FOV, Field of View):控制视野的垂直角度。
- 宽高比(Aspect Ratio):视口的宽度与高度的比值。
- 近平面(Near)和远平面(Far):定义可视深度范围。
视锥体的几何形状:
近平面较小(靠近相机),远平面较大,形成向远处发散的锥形结构。
$$ M_{per}=\begin{bmatrix} \frac{2n}{r-l} &0 & \frac{r+l}{r-l}& 0\\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} &0 \\ 0 & 0 & \frac{f+n}{n-f} &\frac{2fn}{f-n} \\ 0 & 0 & 1 &0 \end{bmatrix} $$
