物理学|[力学] 机械运动
机械运动简介
机械运动是物理学中最基础也是最直观的概念之一,它描述了物体在空间中的位置随时间变化的现象(当物体不满足该条件时就不是机械运动)。无论是天上飞鸟的翱翔、地上车辆的行驶,还是原子内部粒子的震动,都可以被归类为机械运动的研究对象。
下面介绍一下机械运动中几个重要的概念
坐标系 (Coordinate System)
物体在空间中的位置由坐标系决定,所以坐标系是用于定量描述物体在空间中的位置、运动以及其他物理量的数学工具。这个坐标系与数学中的坐标系别无二样,只是把数学工具用于实际世界。坐标系的选取是任意的选择不同的坐标系去描述物体的运动结果还是一样的(读者自行证明)。
运动 (Motion)
运动是指一个物体相对于另一个物体的位置随时间发生改变的过程。在日常生活中,我们可以通过观察物体相对于另一个物体的位置来判断它是否处于运动状态。然而,在物理学中,我们需要更加精确地定义和描述运动,这就引入了几个重要的概念:质点、参考系、位移、速度和加速度。
- 质点 (Point Mass): 在研究物体的运动时,如果物体的尺寸和形状对问题的影响可以忽略不计,我们可以将该物体简化为一个没有大小和形状、仅有质量的几何点,这样的理想化模型(这种思想在以后可能会经常出现)被称为质点(不将其理想为质点的会根据物质的性质进行分类研究,如流体,刚体等)。质点的引入大大简化了对物体运动的分析,使我们能够集中注意力于物体整体的运动特性,而不必考虑其内部结构或复杂形态。例如,在研究地球绕太阳公转时,由于地球与太阳之间的距离远大于地球本身的尺寸,因此可以将地球视为质点。
位移 (Displacement): 位移是一个矢量(向量),表示物体从初始位置到最终位置之间的直线距离及其方向。不同于路程,位移关注的是起点和终点之间的直接路径。其公式为:
$$ \Delta x = \overrightarrow{OB}-\overrightarrow{OA} ,其中\overrightarrow{OA}为起始坐标,\overrightarrow{OB} 为终点坐标 $$
举几个例子来加深对位移的理解
例1:小爱围绕标准跑道跑步,从A点起跑,跑了一圈恰好回到A点,他的位移是多少,路程是多少?
$$ \begin{array}{c} 路程是跑道的周长为400m\\ 根据位移公式其位移为\\ \Delta x = \overrightarrow{OA}- \overrightarrow{OA} = \vec{0} \end{array} $$
速度 (Velocity): 速度也是一个矢量,它表示物体位移的变化率,即单位时间内物体位置的变化率。速度等于位移对时间的导数。其公式为:
$$ \begin{array}{c} 瞬时速度公式:v(t) = \frac{\mathrm{d} x(t)}{\mathrm{d} t} \\ 平均速度公式:\bar{v} = \frac{\Delta x}{\Delta t} \end{array} $$
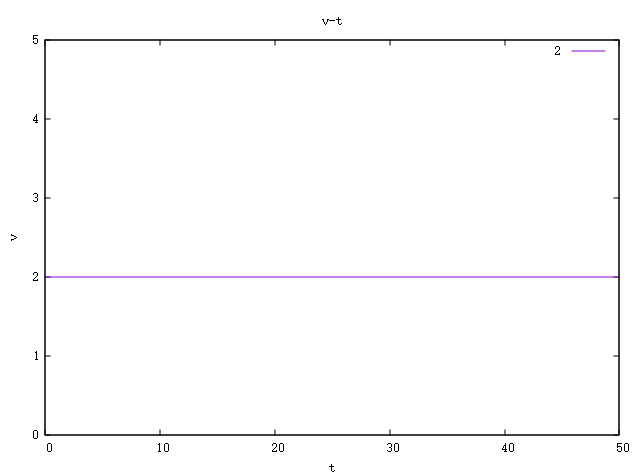
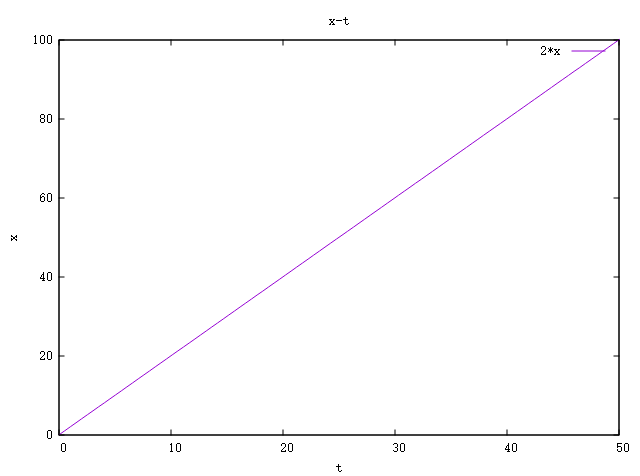
例2:小爱跑步时有一段跑道为直线,小爱在通过直线跑道时其位移关于时间的函数为x(t)=2t m 求其这一过程的速度关于时间的函数。
$$ \begin{array}{c} 根据速度公式其速度函数为\\ v(t) = \frac{\mathrm{d} x(t)}{\mathrm{d} t} = \frac{\mathrm{d} (2t~m)}{\mathrm{d} t} = 2~m/s \end{array} $$
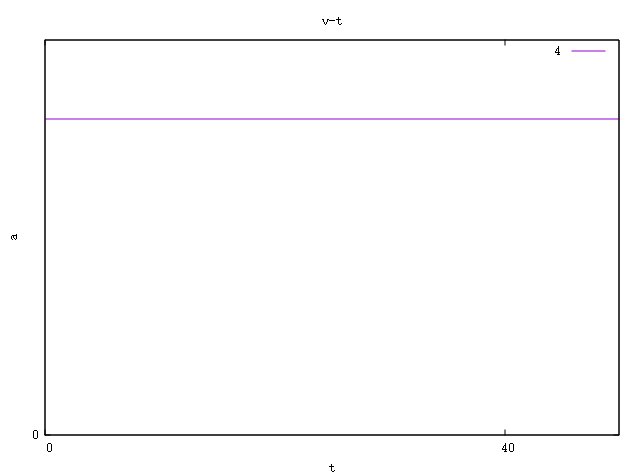
可以看到这一过程的速度函数是一个不变的常数,对于速度不变(大小与方向都不能变,即速度向量不能变)的运动我们称之为匀速运动。
其图像为:
加速度 (Acceleration): 加速度同样是矢量,它表示速度变化的快慢,即单位时间内速度的变化。如果物体的速度大小或方向发生变化,那么该物体就有加速度。其公式为:
$$ \begin{array}{c} 瞬时加速度公式:a(t) = \frac{\mathrm{d} v(t)}{\mathrm{d} t} \\ 平均加速度公式:\bar{a} = \frac{\Delta v}{\Delta t} \end{array} $$
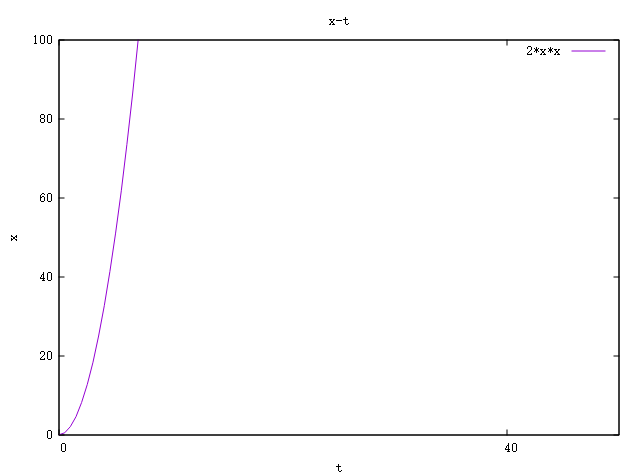
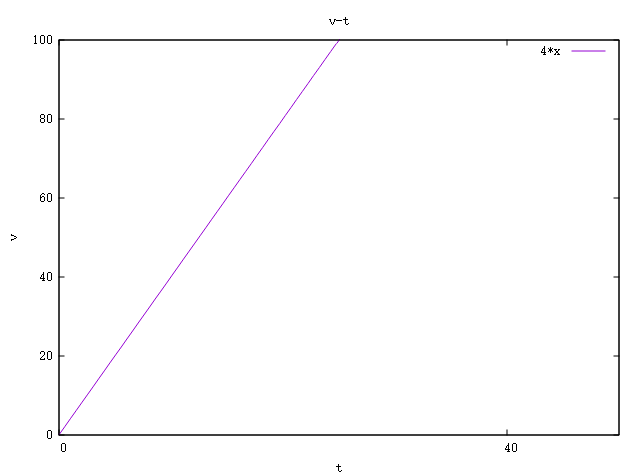
例3:小爱跑步时有通过一个弯曲的跑道,小爱在通过弯曲跑道时其位移关于时间的函数为x(t)=2t*t m 求其这一过程的加速度关于时间的函数。
$$ \begin{array}{c} 根据加速度公式其加速度函数为\\ a(t) = \frac{\mathrm{d} v(t)}{\mathrm{d} t} = \frac{\mathrm{d^{2} } x(t)}{\mathrm{d} t^{2}} = \frac{\mathrm{d^{2}}(2t^{2}~m) }{\mathrm{d} t^{2}} = 4~m/s^{2} \end{array} $$
参考系 (Reference Frame)
为了准确描述物体的运动,必须选择一个参考系,也就是用来衡量物体位置变化的标准框架。参考系可以是固定的,比如地面;也可以是移动的,如行驶中的火车。选择不同的参考系可能会导致对同一物体运动的不同描述。例如,当你坐在一列高速行驶的列车上阅读一本书时,对于你而言书是静止的(因为你选择了列车作为参考系),但对于站在站台上的人来说,这本书连同你一起在快速移动(他们选择了地面作为参考系)。
相对运动 (Relative Motion)
相对运动指的是两个物体或者两个参考系之间相互运动的状态。
- 当我们说一个物体相对于另一个物体运动时,实际上是在比较这两个物体在同一个参考系下的位置变化。例如,两艘船在海面上相向而行,从一艘船上的人看另一艘船,会认为对方正朝自己快速接近;但从岸上的观察者来看,两艘船都在移动。
当我们说一个系统和相对于另一个系统运动时,实际上是在说系统S中所有的物体相对于系统S‘中所有的物体的位置变换。例如,汽车A与汽车B的相对运动就是汽车A中所有的物体相对于汽车B中所有的物体的位置变化。
因此,理解相对运动有助于我们分析复杂的多体系统,尤其是在交通、航空航天等领域。
