碰撞检测 <图元测试>|基本图元测试

在碰撞检测中处理相交分离需要用到一些辅助方法，例如判断两个点之间的距离有多远，点距离边有多远，点距离面有多远，两条平行线段之间有多远，两个面之间有多远，直线与直线是否相交等等测试。所以我们现在需要实现这些功能，由于我们的游戏引擎是2D的所以我们的工作量相对于3D会减少很多。

点与点之间的距离

这个相信大家都会，中学的时候我们都学过两点之间的距离即欧几里得距离，公式如下：

$$ A(x_{1},y_{1}),B(x_{2},y_{2}),Distance(\overline{AB}) = \sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}} $$

点与直线之间的距离

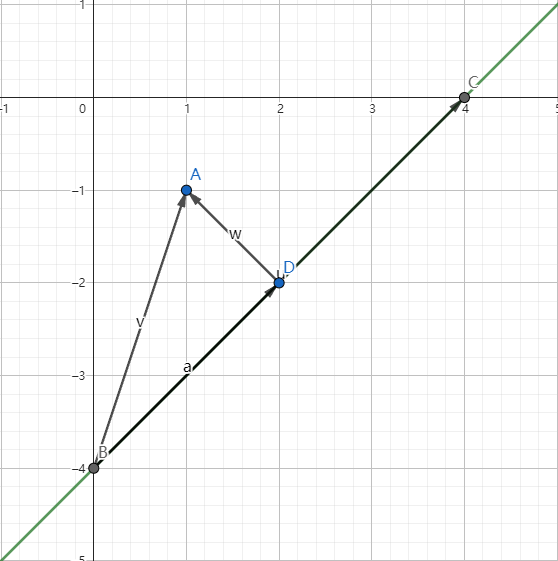
点与直线之间的距离中学的时候也学了，有两种计算方式，其中一种是公式法另一种是向量法，公式法需要使用直线的直线方程不便操作，我们使用第二种方式向量法。

步骤

随便在直线上取一个向量(BC)
在BC这个向量随便选一个端点连接到点A构成向量BA
做向量BA在直线上的投影向量BD
使用BA-BD计算得向量DA
对DA取模就是点A到直线的距离了

直线与直线之间的距离（不相交）

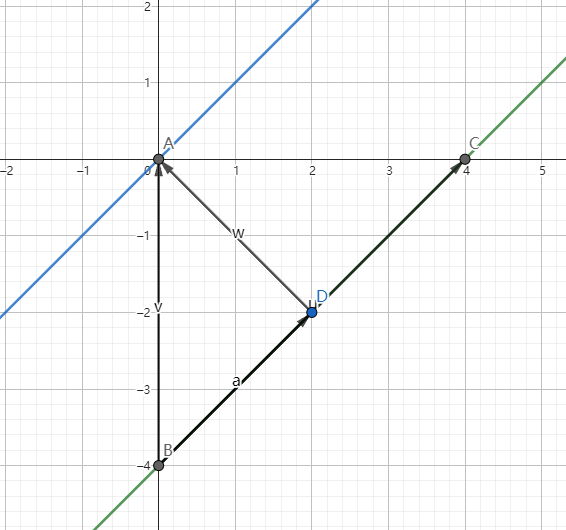
直线与直线之间的距离中学的时候也学了，有两种计算方式，其中一种是公式法另一种是向量法，公式法需要使用直线的直线方程不便操作，我们使用第二种方式向量法。

步骤

在其中一条直线上找到一个点
将问题转化为点到直线之间距离

点到AABB包围盒的最近距离

这需要考虑两种情况

点在AABB包围盒外
点在AABB包围盒上/内

点在AABB包围盒外

先判断点是否在AABB外（点与矩形的相交检测）
计算点距离AABB的距离

这里有一种很奇妙的方式可以计算其距离

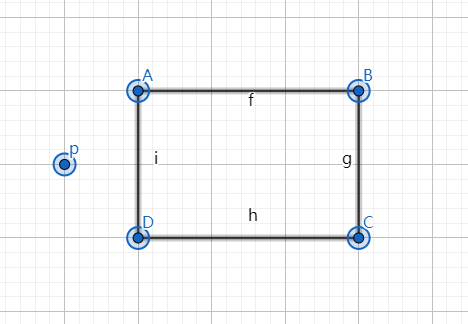
这里需要用到三个点P、D、B;

我们可以这么计算

float distPointAABB(FlatVector p, std::vector<FlatVector> vertices_aabb) {
    float sqDist = 0.0f;
    for (int i = 0; i < 2; i++) { 
        float v,min,max;
        if(i==0)
        {
            v = p.x ;
            min = vertices_aabb[3].x;
            max = vertices_aabb[1].x;
            /*当i为0时对应x 
            v设置为点 p 的 x 坐标。
            min 设置为边界框左上角点的 x 坐标（vertices_aabb[3].x）。
            max 设置为边界框右下角点的 x 坐标（vertices_aabb[1].x）。*/
        }
        if(i == 1) 
        {
            v = p.y;
            min = vertices_aabb[3].y;
            max = vertices_aabb[1].y;
            /*当i为1时对应y
            v设置为点 p 的 y 坐标。
            min 设置为边界框左上角点的 y 坐标（vertices_aabb[3].y）。
            max 设置为边界框右下角点的 y 坐标（vertices_aabb[1].y）。y*/
        }
        if (v < min) sqDist += (min - v) * (min - v);
        if (v > max) sqDist += (v - max) * (v - max);
    }
    return std::sqrt(sqDist); // 计算平方根
}

解释：