类型一：一部分与其他用电器并联一部分位于干路上

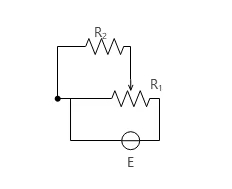
设R1=h,R2=c,R1与R2并联的部分设为b，R1位于干路部分设为a

我们可以列出以下方程

$$ a+b=h $$

$$ R_总=\frac{bc}{b+c} + h-b=\frac{-b^2+bh+hc}{b+c} =\frac{-b^2}{b+c}+h $$

这里R总可以看为b关于f(b)的函数及

$$ f(b)=\frac{-b^2}{b+c}+h ,(0\le b\le h) $$

画出图像可知随着滑动变阻器并联的部分越多，总电阻越小。即在此情况下并联部分与总电阻成反比

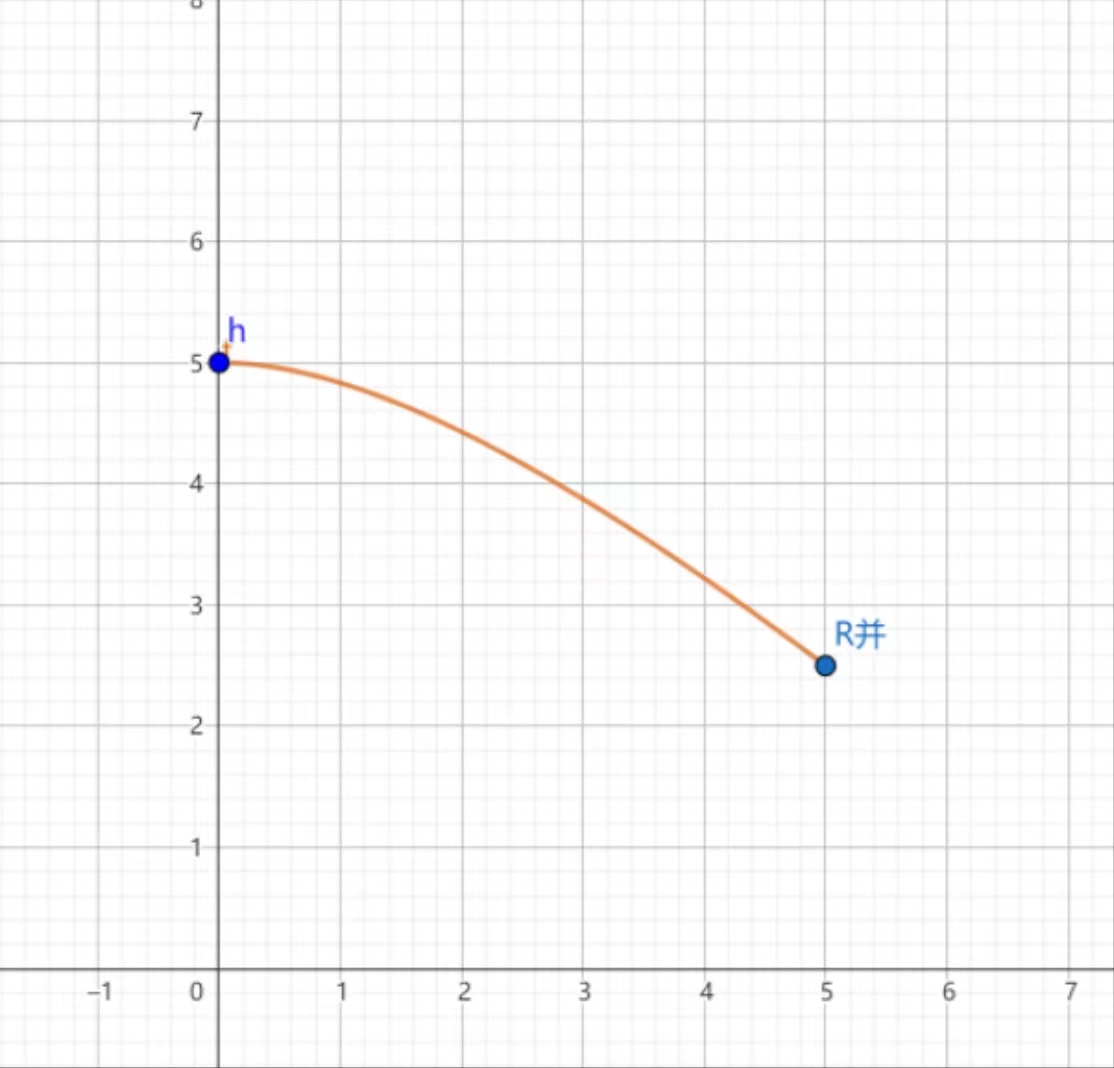
若没有画图软件可自行求导画图

类型二：两部分分别并联在不同支路上

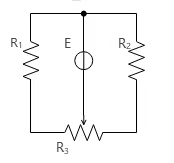
设R1=a，R2=b，R3=c，R3中与R1并联的部分RL设为d，R3中与R3并联的部分RR设为e

我们可以列出以下方程

$$ d+e=c $$

$$ d=kc $$

$$ R_总=\frac{(a+d)(b+e)}{a+b+c}=\frac{(a+kc)(b+c(1-k))}{a+b+c} $$

$$ R_总=-\frac{c^2}{a+b+c}k^2+(\frac{cb-ac+c^2}{a+b+c} ) k+\frac{ac+ab}{a+b+c} $$

同样这里R总可以看为k关于f(k)的函数及

$$ f(k)=Ak^2+Bk+C(0\le k \le 1 ) $$

其中

$$ A=-\frac{c^2}{a+b+c},B=\frac{cb-ac+c^2}{a+b+c},C=\frac{ac+ab}{a+b+c} $$

当k=0时有

$$ R_总=\frac{a(c+b)}{a+b+c} $$

当k=1时有

$$ R_总=\frac{b(c+a)}{a+b+c} $$

当

$$ k=\frac{b-a+c}{2c} $$

时R总有最大值，怎么判断R总最大时k是否位于定义域中

我们进行如下变形

$$ k=\frac{b-a}{2c}+\frac{1}{2} $$

所以我们只需要知道什么情况下满足以下不等式就行

$$ -\frac{1}{2} \le \frac{b-a}{2c}\le \frac{1}{2} $$

解得

$$ c\ge \left | a-b \right | $$

即满足以上不等式R有极大值

可推得以下结论

$$ b-a+c=2kc $$

$$ b-a+d+e=2d $$

$$ d+a=e+b $$

即

$$ R_L+R_1=R_R+R_2 $$

若不满足则当k=1时R总最大

或者令

$$ d=(1-k)c $$

时k=0时取得R总最大

即滑动变阻器拉满时R总最大