前言

在我们介绍人工神经元的时候提到了人工神经元模型是模仿生物体的神经元进行设计的模型。在那一篇文章中我们了解到生物神经元中的电信号在达到阈值时才会输出电信号给下一个神经元。人工神经元为了模仿生物神经元这一特征在人工神经元中加入了激活函数（Activation functions）

这篇文章你将会了解：

什么是激活函数
常用的激活函数
使用python编写带有激活函数的神经元完成非线性回归

什么是激活函数

由于我们之前的神经元只有一段线性函数y=wx+b，没有激活函数的神经网络实质上是一个线性回归模型，只能解决线性可分的问题，而对于线性不可分的任务我们之前的神经元就无能为力了，这时候我们就引入了激活函数，使得我们的函数变得不线性也就是变成非线性函数，这可以增加模型泛化能力。

例如我们不可能用一条直线去拟合这种分布的数据：

而曲线可以

所以激活函数能够帮助你的神经元完成更加复杂的工作。

并且我们人类思考问题的过程并不是完美的拟合，而是离散的分类，我们会给食物能否吃饱分成多类：能吃饱，不能吃饱，能吃几分饱(这也是我们根据经验得出的新类)，而我们并不会去使用一个食物的大小和饱腹程度的函数去判断是否能吃饱。

我们把之前线性函数的输出放入激活函数中计算后的值做出最后的输出

常见的激活函数

sigmoid

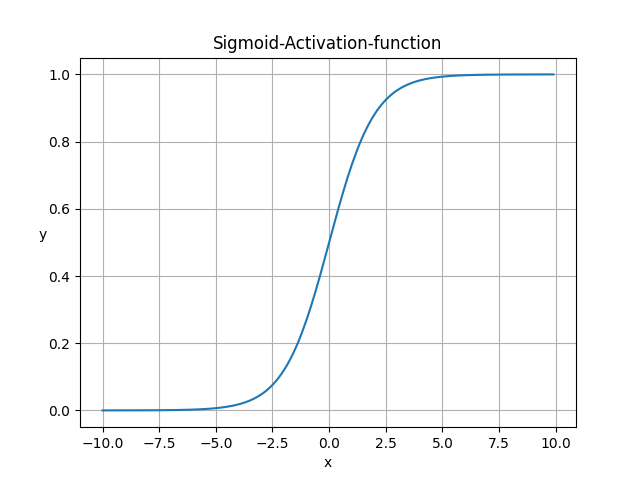
$$ sigmoid(x) = \frac{1}{1+e^{-x} } $$

sigmoid激活函数特点：

把(−∞,+∞)的数映射到(0,1)之间，因此它对每个神经元的输出进行了归一化；
Sigmoid 函数非常合适用于将预测概率作为输出的模型。因为概率的取值范围是 0 到 1。
函数处处可导。
函数很快逼近y=0和y=1，导数无限小，这会导致权重更新的非常慢
一般用于二分类的输出层

sigmoid的导函数

$$ \frac{\partial sigmoid(x)}{\partial x} = sigmoid(x)(1-sigmoid(x)) $$

Tanh

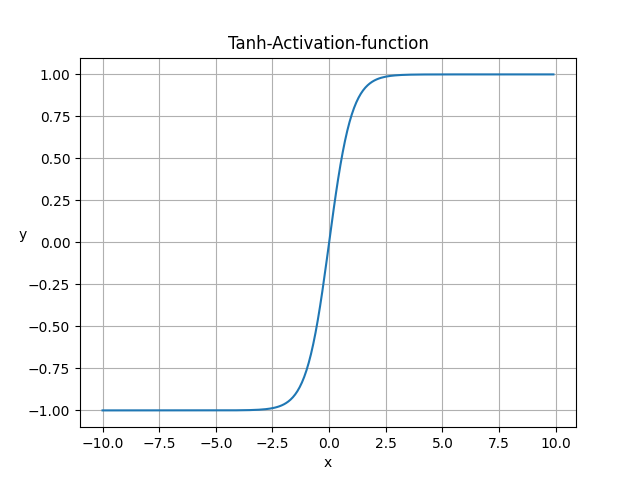
$$ Tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x} } $$

Tanh激活函数特点：

函数是将取值为 (−∞,+∞) 的数映射到(−1,1) 之间；
在0附近的导数相比sigmoid更大，收敛速度比sigmoid快
函数处处可导。
函数很快逼近y=0和y=1，导数无限小，这会导致权重更新的非常慢

Tanh的导函数

$$ \frac{\partial Tanh(x)}{\partial x} = 1-Tanh(x)^{2} $$

ReLU

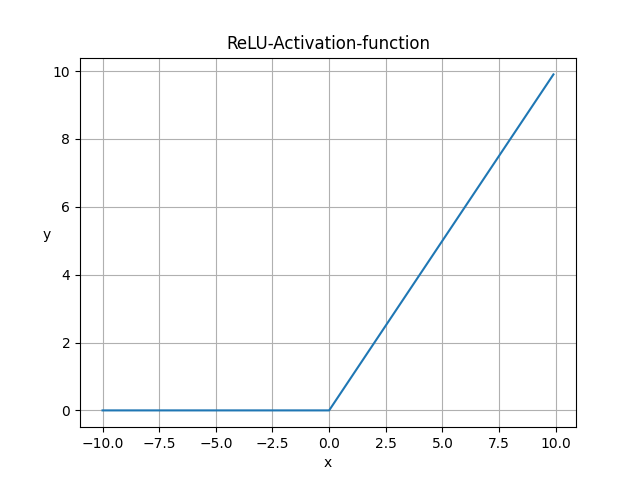
$$ ReLU(x) = \begin{cases} 0 & x\leqslant 0 \\ x & x>0 \end{cases} $$

ReLU激活函数特点：

计算简单高效，相比sigmoid、tanh没有指数运算
相比sigmoid、tanh更符合生物学神经激活机制
收敛速度较快，大约是 sigmoid、tanh 的 6 倍
在x<0时导数为0，这会导致权重参数无法得到更新，这被称为神经元死亡，或者梯度消失

ReLU的导函数

$$ \frac{\partial ReLU(x)}{\partial x} = \begin{cases} 0 & x\leqslant 0 \\ 1 & x>0 \end{cases} $$

使用python编写带有激活函数的神经元完成非线性回归

只使用Sigmoid完成

# 导入numpy库
import numpy as np
from matplotlib import pyplot as plt


def sigmoid(x):
    return 1/(1+np.exp(-x))


def sigmoid_deriv(a):
    return a*(1-a)


def getdata(count):
    """获取指定数量的数据"""
    xs = np.random.rand(count)
    xs = np.sort(xs)
    ys = np.zeros(count)
    for i in range(count):
        x = xs[i]
        yi = 0.7*x+(0.5-np.random.rand())/50+0.5
        if yi > 0.8:
            ys[i] = 1
    return xs, ys


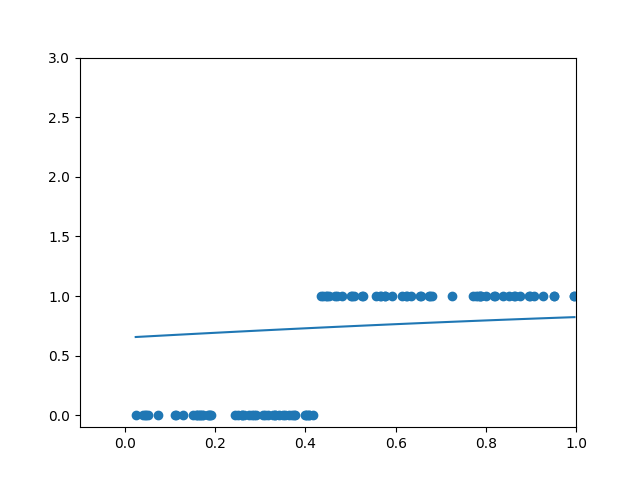
data = getdata(100)
xs = data[0]
ys = data[1]

w = np.random.rand(1)
b = np.random.rand(1)
z = w*xs+b
a = sigmoid(z)

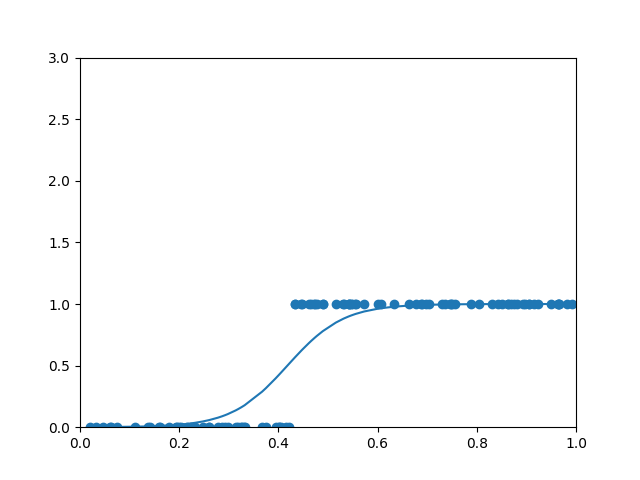
plt.xlim(-0.1, 1)
plt.ylim(-0.1, 3)
plt.scatter(xs, ys)
plt.plot(xs, a)
plt.show()

for j in range(1000):
    for i in range(len(xs)):
        x = xs[i]
        y = ys[i]
        # 前向传播
        z = w*x+b
        a = sigmoid(z)#加入激活函数
        e = (y - a)**2

        alpha = 0.05

        # 反向传播
        deda = -2*(y-a)
        dadz = sigmoid_deriv(a)#加入激活函数后本质还是复合函数求导
        dzdw = x
        dzdb = 1

        dedw = deda*dadz*dzdw
        w = w - alpha*dedw
        dedb = deda*dadz*dzdb
        b = b - alpha*dedb

z = w*xs+b
a = sigmoid(z)
plt.xlim(0, 1)
plt.ylim(0, 3)
plt.scatter(xs, ys)
plt.plot(xs, a)
plt.show()

给神经元加入激活函数