物理必修二期中总结
第一章 抛体运动
第一节 曲线运动
- 曲线运动的定义:物体运动轨迹是曲线时,我们就称这个物体做的是曲线运动。
- 关于曲线运动的速度方向:物体做曲线运动时,速度方向会不停改变,速度的方向为某时刻在轨迹的切线方向上。
- 物体在什么情况下做曲线运动:通过大量实验证明当物理所受到的力或自己的加速度与物理的速度方向不在同一条直线上时物理做曲线运动。根据牛顿第一定律可知物体肯定是受到了一个力,迫使它的运动状态发生了变化。根据牛顿第二定律可知有力必然有加速度,有加速度物体的速度一定会发生改变。当加速度或力与物体的速度方向在同一直线上时,物体做匀变速直线运动。反之,不在同一直线上时做曲线运动。
总结
- 有加速度/有力并且与速度方向不在同一直线上物体做曲线运动
- 物体做曲线运动时,加速度/力总直线运动轨迹凹的那一侧(指向内部)
- 当物体的速度方向与力/加速度的方向夹角为锐角时物体做速度变大的曲线运动
- 当物体的速度方向与力/加速度的方向夹角为钝角时物体做速度变小的曲线运动
- 当物体的速度方向与力/加速度的方向夹角为直角时物体做速度不变的曲线运动(匀速圆周运动)
------
第二节 运动的合成与分解
- 将曲线运动分解为多段直线运动:在物理学中我们经常将复杂的问题转化为简单的问题再来进行分析(等效替代法)
- 分解速度:通过大量实验证明,我们可知不同方向上的速度不会影响其他方向上的运动(独立性)。所以我们可以把他们拆成多个分运动进行分析。
- 如何分解速度:只要是矢量都遵循平行四边形法则,通过平行四边形法则将速度,位移,力等矢量进行分解。
速度合成:
- 匀速直线+匀速直线=匀速直线
- 匀速直线+匀加速直线=曲线运动
- 匀加速直接+匀加速直线=曲线/直线运动(如果两个分加速度合成出来的合加速度在物体的合速度方向上,物体做直线,反之曲线)
小船过河问题(只研究船速大于水速的情况下)

总结
- 将曲线运动分解为多段直线运动进行分析(等效替代法)
- 同一个物体多段分运动加起来的效果与合运动的效果一致(等效性)
- 同一个物体的多段分运动都是同时进行(等时性)
- 同一个不同方向上分运动不会影响其他方向分运动(独立性)
------
第三节 平抛运动
**
- 定义:物体在一定高度以水平初速度抛出,在只受重力的作用下做的运动叫做平抛运动(理想模型,忽略了空气阻力)
- 分析:将物体的运动分解,物体抛出后在水平方向上不受力所以做匀速直线运动,在竖直放方向只受重力作用并且竖直方向上初速度为零所以竖直方向上做自由落体运动。
平抛运动的规律:
水平方向上 竖直方向上 频闪照片水平方向上 频闪照片竖直方向上 位移 x=v₀t y=1/2gt² 数格子 数格子 速度 vₓ=v₀ vᵧ=gt vₓ=X/(ΔY/g)^0.5 vᵧ=(Δyg)^0.5 - 水平分速度与合速度的正切值是水平位移与合位移的正切值得两倍
第四节 生活中的抛体运动
竖直上抛运动
- 特点:最高点速度为0、具有对称性,抛出后只受重力影响。
斜抛运动
- 特点:分解为竖直上抛运动与匀速直线运动来分析、45度角水平位移最大、只受重力影响。
第二章 圆周运动
第一节 匀速圆周运动
圆周运动
当物体的运动轨迹是圆的时候那么这个物体做的就是圆周运动
线速度
物体通过的弧长与时间的比可以用来描述物体做圆周运动的快慢,通常指的是物体此刻的瞬时速度。
定义式$$V=\frac{\Delta L}{\Delta t}$$方向为该点的切线方向。因为物体做的是圆周运动,所以速度方向一定改变,单位“m/s”。
匀速圆周运动
物体做圆周运动时,任意相等时间内通过的弧长相等那么这个物体做的就是匀速圆周运动,此时物体的线速度大小不变
角速度
物体通过弧度与时间的比可以用来描述物体做圆周运动的快慢
定义式\omega = \frac{\theta }{\Delta t}方向用右手螺旋定则确定,单位是“rad/s”
周期
指物体做匀速圆周运动转一圈所用的时间,一般用字母
T表示,单位’s‘转速
指物体做匀速圆周运动时运动一秒所转过的圈数,一般用字母
n表示,单位r/s、圈每秒$$n=f$$
频率
周期的倒数(每秒内完成周期性运动的次数)叫频率,一般用字母
f表示,单位Hz$$f=\frac{1}{T}$$
关系式
在匀速圆周运动中有:
$$V=\frac{2\pi r}{T}=2\pi rn=2\pi rf$$
$$\omega = \frac{2\pi }{T}=2\pi n=2\pi f$$
$$V=\omega r$$
第二节 向心力与向心加速度
向心力是指物体沿圆周轨道运行时,指向圆心的合外力作用力
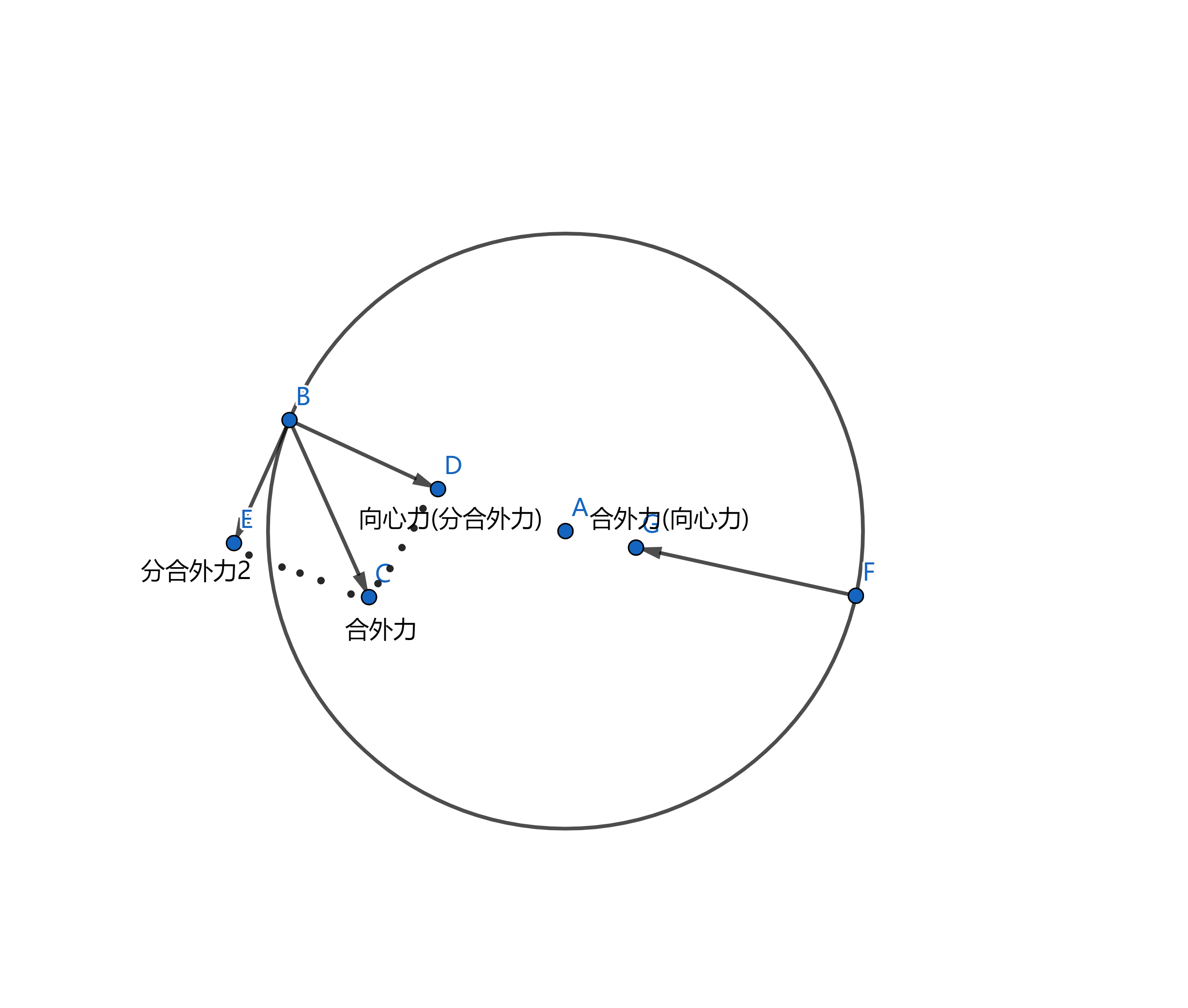
公式$$F=m\omega ^{2}r=m\frac{v^{2}}{r}=m\frac{4\pi ^{2}}{T^{2}}r=m4\pi ^{2}n^{2}r=m4\pi ^{2}f^{2}r=m\omega v$$
根据牛顿第二定律推得$$a=\frac{F}{m}=\omega ^{2}r=\frac{v^{2}}{r}=\frac{4\pi ^{2}r}{T^{2}}=v\omega =4\pi ^{2}f^{2}r=4\pi ^{2}n^{2}r$$方向与向心力方向一致
在匀速圆周运动中向心加速度并不会改变速度大小只会改变速度方向
- 关于圆周运动的一些模型

待更新
